题目内容
函数y=|x-2|+3的图象的对称轴为 ．
考点：带绝对值的函数
专题：函数的性质及应用
分析：函数y=|x|为偶函数，对称轴为y轴，其图象向右平移2个单位，再向上平移3个单位后，可得函数y=|x-2|+3的图象，进而得到对称轴方程．
解答：
解：函数y=|x|为偶函数，对称轴为y轴，
其图象向右平移2个单位后，可得函数y=|x-2|的图象，对称轴为直线x=2，
其图象向上平移3个单位后，可得函数y=|x-2|+3的图象，对称轴仍为直线x=2，
故答案为：x=2．
其图象向右平移2个单位后，可得函数y=|x-2|的图象，对称轴为直线x=2，
其图象向上平移3个单位后，可得函数y=|x-2|+3的图象，对称轴仍为直线x=2，
故答案为：x=2．
点评：本题考查的知识点是函数图象的对称性，函数图象的平移变换，熟练掌握函数图象变换“左加右减，上加下减”的原则是解答的关键．
练习册系列答案
相关题目
复数
的值是（ ）
| 1+i |
| 1-i |
| A、0 | B、1 | C、-1 | D、i |
已知函数y=f（x）的定义域是数集A，若对于任意a，b∈A，当a＜b时，都有f（a）＜f（b），则方程f（x）的实数根为（ ）
| A、有且只有一个 |
| B、一个都没有 |
| C、至多有一个 |
| D、可能会有两个或两个以上 |
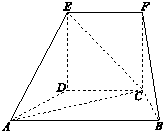如图所示的几何体中，面CDEF为正方形，面ABCD为等腰梯形，AB∥CD，AB=2BC，∠ABC=60°，且平面CDEF⊥平面ABCD．