题目内容
设a、b、c>0,证明:
+
+
+
≥
.
| a |
| b+c |
| b |
| a+c |
| c |
| a+b |
|
| 5 |
| 2 |
考点:不等式的证明
专题:证明题,不等式的解法及应用
分析:由于a、b、c>0,运用二元均值不等式,即可得到a2+b2+c2≥ab+bc+ca,即有
≥1,再对
+
+
的分子常数化,再由三元均值不等式,即可得到
+
+
≥
,进而得到证明.
|
| a |
| b+c |
| b |
| a+c |
| c |
| a+b |
| a |
| b+c |
| b |
| a+c |
| c |
| a+b |
| 3 |
| 2 |
解答:
证明:由于a、b、c>0,a2+b2≥2ab,
b2+c2≥2bc,c2+a2≥2ca,
相加,得a2+b2+c2≥ab+bc+ca,
即有
≥1,当且仅当a=b=c取等号,①
又
+
+
=
+
+
=(a+b+c)(
+
+
)-3=
((c+b)+(c+a)+(a+b))(
+
+
)-3
≥
•3
•3
-3=
-3=
,当且仅当a=b=c取等号,②
①+②,得,
+
+
+
≥
.
b2+c2≥2bc,c2+a2≥2ca,
相加,得a2+b2+c2≥ab+bc+ca,
即有
|
又
| a |
| b+c |
| b |
| a+c |
| c |
| a+b |
| a+b+c-(b+c) |
| b+c |
| a+b+c-(a+c) |
| a+c |
| a+b+c-(a+b) |
| a+b |
=(a+b+c)(
| 1 |
| c+b |
| 1 |
| c+a |
| 1 |
| a+b |
| 1 |
| 2 |
| 1 |
| c+b |
| 1 |
| c+a |
| 1 |
| a+b |
≥
| 1 |
| 2 |
| 3 | (c+b)(c+a)(a+b) |
| 3 |
| ||
| 9 |
| 2 |
| 3 |
| 2 |
①+②,得,
| a |
| b+c |
| b |
| a+c |
| c |
| a+b |
|
| 5 |
| 2 |
点评:本题考查不等式的证明,考查均值不等式的运用,注意变形,考查推理能力,属于中档题.

练习册系列答案
相关题目
设U为全集,A∩B=∅,则B∩(∁UA)为( )
| A、A | B、B |
| C、∁UB | D、∅ |
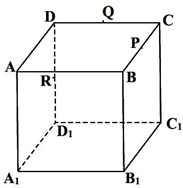 如图,正方体ABCD-A1B1C1D1的棱长为2,P,Q,R分别是棱BC,CD,DD1的中点.下列命题:
如图,正方体ABCD-A1B1C1D1的棱长为2,P,Q,R分别是棱BC,CD,DD1的中点.下列命题: