题目内容

在△ABC中，AB=
15
，AC=2，BC=3，点D在BC边上，BC=2CD，则
AD
•
.
BC
=（　　）
A、6B、-6C、4D、-4
考点：平面向量数量积的运算
专题：计算题,解三角形,平面向量及应用
分析：运用向量的共线知识，可得
AD
=
1
3
AB
+
2
3
AC
，又
BC
=
AC
-
AB
，再由向量的数量积的定义和性质：向量的平方即为模的平方，计算即可得到所求值．
解答： 解：由点D在BC边上，BD=2CD，
则D为BC的三点分点，
即
BD
=2
DC
，
有
AD
-
AB
=2（
AC
-
AD
），
则
AD
=
1
3
AB
+
2
3
AC
，
则
AD
•
.
BC
=（
1
3
AB
+
2
3
AC
）•（
AC
-
AB
）
=
2
3
AC
2-
1
3
AB
2-
1
3
AB
•
AC

=
2
3
×4-
1
3
×15-
1
3
×2
15
cosA
=
8
3
-5-
2
15
3
×
4+15-9
2×2
15
=-4．
故选D．
点评：本题考查平面向量的运用，考查向量的共线表示形式，考查向量的数量积的定义和向量的平方即为模的平方，考查运算能力，属于中档题．
练习册系列答案
相关题目
设集合A={x|-4＜x＜3}，B={x|x≤2}，则A∪B=（　　）
A、（-4，3）
B、（-4，2]
C、（-∞，2]
D、（-∞，3）
已知等比数列{an}的前n项和为Sn，且a1=2，an+1=Sn+
t
16
（n∈N+，t为常数）．
（Ⅰ）求t的值及数列{an}的通项公式；
（Ⅱ）已知bn=n（n∈N*），记Tn为{bn•an}的前n项和，若（n-1）2≤m（Tn-n-1）对于n≥2恒成立，求实数m的范围．
已知球的表面积为16π，则该球的体积为
 
．
若几何体的三视图如图所示，则该几何体的体积为（　　）
A、
π
6
B、
π
3
C、
2π
3
D、π
已知a＞0，b＞0，则下列不等式中不恒成立的是（　　）
A、
ab
≥
2ab
a+b
B、（a+b）（
1
a
+
1
b
）≥4
C、
|a-b|
≥
a
-
b
D、a2+b2+1≥2a+2b
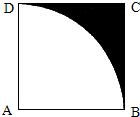如图，在边长为1的正方形ABCD中，以A为圆心，AB为半径作扇形ABD，在该正方形内随机取一点，则此点取自阴影部分的概率是
 
．
某商场经营一批进价是每件30元的商品，在市场销售中发现此商品的销售单价x元（30≤x≤50）与日销售量y件之间有如下关系：
销售单价x（元）30404550
日销售量y（件）6030150
（Ⅰ）经对上述数据研究发现，销售单价x与日销售量y满足函数关系y=kx+b，试求k，b的值；
（Ⅱ）设经营此商品的日销售利润为P元，根据（Ⅰ）关系式，写出P关于x的函数关系式，并求出销售单价x为多少元时，才能获得最大日销售利润，最大日销售利润是多少？
已知向量
a
=（x，2），
b
=（1，1），若（
a
+
b
）⊥
b
，则x=（　　）
A、2B、4C、-4D、-2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网