题目内容

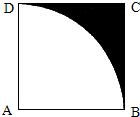如图，在边长为1的正方形ABCD中，以A为圆心，AB为半径作扇形ABD，在该正方形内随机取一点，则此点取自阴影部分的概率是
 
．
考点：几何概型
专题：计算题,概率与统计
分析：根据题意，易得正方形ABCD的面积为1×1=1，阴影部分的面积为1-
π
4
，进而由几何概型公式计算可得答案．
解答： 解：根据题意，正方形ABCD的面积为1×1=1，
阴影部分的面积为1-
π
4
，
则正方形OABC中任取一点P，点P取自阴影部分的概率为1-
π
4
，
故答案为：1-
π
4
．
点评：本题考查几何概型的计算，涉及圆的面积在求面积中的应用，关键是正确计算出阴影部分的面积．
练习册系列答案
相关题目
过原点O的直线MN与双曲线C：
x2
a2
-
y2
b2
=1交于M、N两点，P是双曲线C上异于M、N的点，若直线PM，PN的斜率之积kPM•kPN=
5
4
，则双曲线C的离心率e=（　　）
A、
3
2
B、
9
4
C、
5
4
D、2
已知正方体ABCD-A1B1C1D1，E、F分别是AB、AD中点，则异面直线EF与A1C1所成的角为（　　）
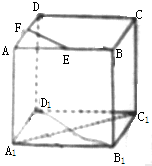
A、30°B、45°
C、60°D、90°
在△ABC中，AB=
15
，AC=2，BC=3，点D在BC边上，BC=2CD，则
AD
•
.
BC
=（　　）
A、6B、-6C、4D、-4
下列不等式不成立的是（　　）
A、a2+b2+c2≥ab+bc+ca
B、
a
+
b
＞
a+b
（a＞0，b＞0）
C、
a
-
a-1
＜
a-2
-
a-3
（a≥3）
D、
2
+
10
＞2
6
在极坐标系中，点P（2，-
π
3
）到直线l：ρsin（θ-
π
6
）=1的距离是
 
．
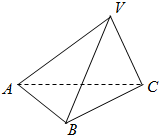如图，三棱锥V-ABC的底面是以B为直角顶点的等腰直角三角形，侧面VAC与底面ABC垂直，已知其正视图的面积为2
3
，则其侧视图的面积是（　　）
A、
3
2
B、
3
C、2
3
D、3
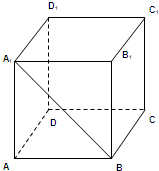如图，ABCD-A1B1C1D1为正方体．
（1）与直线AB异面的直线有哪些？
（2）求A1B与直线CD所成角的大小．
已知x，y满足约束条件
5x+3y-15≤0
x-y+1≥0
x-5y-3≤0
，则z=3x+5y的最大值为（　　）
A、0B、5C、3D、17

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网