题目内容
已知a＞0，b＞0，则下列不等式中不恒成立的是（ ）
A、
| ||||||
B、（a+b）（
| ||||||
C、
| ||||||
| D、a2+b2+1≥2a+2b |
考点：不等式的基本性质
专题：不等式的解法及应用
分析：A．利用基本不等式的性质即可判断出；
B．利用基本不等式的性质即可判断出；
C．平方作差即可判断出；
D．当a=b=
时，a2+b2+1-2a-2b＜0，即可判断出．
B．利用基本不等式的性质即可判断出；
C．平方作差即可判断出；
D．当a=b=
| 2 |
| 3 |
解答：
解：A．∵a＞0，b＞0，∴
≤
=
，当且仅当a=b时取等号，正确；
B.(a+b)(
+
)≥2
•2
=4，当且仅当a=b时取等号，正确；
C.(
)2-(
-
)2=2
＞0，因此恒成立，正确；
D．当a=b=
时，a2+b2+1-2a-2b=（a-1）2+（b-1）2-1=
-1＜0，因此不恒成立，不正确．
故选：D．
| 2ab |
| a+b |
| 2ab | ||
2
|
| ab |
B.(a+b)(
| 1 |
| a |
| 1 |
| b |
| ab |
|
C.(
| |a-b| |
| a |
| b |
| ab |
D．当a=b=
| 2 |
| 3 |
| 2 |
| 9 |
故选：D．
点评：本题考查了基本不等式的性质、平方作差比较数的大小，考查了计算能力，属于基础题．
练习册系列答案
全程金卷系列答案
相关题目
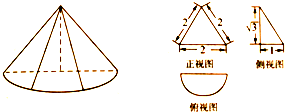已知图（2）是图（1）所示几何体的三视图，其中俯视图是个半圆，则图（1）所示几何体的表面积为（ ）A、
| ||||
B、π+
| ||||
C、
| ||||
D、
|
已知直线m，n和平面α，β，若α⊥β，α∩β=m，n?α，要使n⊥β，则应增加的条件是（ ）
| A、m∥n | B、n∥α |
| C、n⊥m | D、n⊥α |
在△ABC中，AB=
，AC=2，BC=3，点D在BC边上，BC=2CD，则
•
=（ ）
| 15 |
| AD |
. |
| BC |
| A、6 | B、-6 | C、4 | D、-4 |
下列选项中不是右图中几何体的三种视图之一的是（ ）
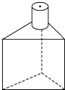
A、 |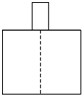
B、 |
C、 |
D、 |
下列函数中，在（-1，1）内有零点且单调递增的是（ ）
A、y=log
| ||
| B、y=-x3 | ||
| C、y=2x-1 | ||
| D、y=x2-2 |