题目内容
已知球的表面积为16π，则该球的体积为 ．
考点：球的体积和表面积
专题：计算题,空间位置关系与距离
分析：通过球的表面积求出球的半径，然后求出球的体积
解答：
解：一个球的表面积是16π，所以球的半径为：2，
所以这个球的体积为：
×23=
π．
故答案为：
π．
所以这个球的体积为：
| 4π |
| 3 |
| 32 |
| 3 |
故答案为：
| 32 |
| 3 |
点评：本题是基础题，考查球的表面积、体积的计算，考查计算能力，公式的应用．
练习册系列答案
相关题目
在空间，下列命题中正确的是 （ ）
| A、没有公共点的两条直线平行 |
| B、与同一直线垂直的两条直线平行 |
| C、平行于同一直线的两条直线平行 |
| D、已知直线a不在平面α内，则直线a∥平面α |
已知直线m，n和平面α，β，若α⊥β，α∩β=m，n?α，要使n⊥β，则应增加的条件是（ ）
| A、m∥n | B、n∥α |
| C、n⊥m | D、n⊥α |
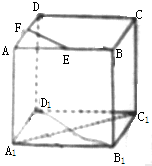
已知正方体ABCD-A1B1C1D1，E、F分别是AB、AD中点，则异面直线EF与A1C1所成的角为（ ）
| A、30° | B、45° |
| C、60° | D、90° |
在△ABC中，AB=
，AC=2，BC=3，点D在BC边上，BC=2CD，则
•
=（ ）
| 15 |
| AD |
. |
| BC |
| A、6 | B、-6 | C、4 | D、-4 |
