题目内容
方程
+
=1表示曲线C,给出以下命题:
①曲线C不可能为圆;
②若曲线C为双曲线,则t<1或t>4;
③若1<t<4,则曲线C为椭圆;
④若曲线C为焦点在x轴上的椭圆,则1<t<
.
其中真命题的序号是 (写出所有正确命题的序号).
| x2 |
| 4-t |
| y2 |
| t-1 |
①曲线C不可能为圆;
②若曲线C为双曲线,则t<1或t>4;
③若1<t<4,则曲线C为椭圆;
④若曲线C为焦点在x轴上的椭圆,则1<t<
| 5 |
| 2 |
其中真命题的序号是
考点:圆锥曲线的共同特征
专题:圆锥曲线的定义、性质与方程
分析:①当4-t=t-1>0,即t=
时,曲线C表示圆;
②若曲线C为双曲线,则(4-t)(t-1)<0,解出即可判断出;
③若4-t>0,t-1>0且4-t≠t-1,解出即可得出曲线C为椭圆;
④若曲线C为焦点在x轴上的椭圆,则4-t>t-1>0.
| 5 |
| 2 |
②若曲线C为双曲线,则(4-t)(t-1)<0,解出即可判断出;
③若4-t>0,t-1>0且4-t≠t-1,解出即可得出曲线C为椭圆;
④若曲线C为焦点在x轴上的椭圆,则4-t>t-1>0.
解答:
解:方程
+
=1表示曲线C,以下命题:
①当4-t=t-1>0,即t=
时,曲线C表示圆,因此不正确;
②若曲线C为双曲线,则(4-t)(t-1)<0,解得t<1或t>4,正确;
③若4-t>0,t-1>0且4-t≠t-1,解得1<t<4且t≠
,则曲线C为椭圆,因此不正确;
④若曲线C为焦点在x轴上的椭圆,则4-t>t-1>0,解得1<t<
,正确.
综上可得真命题为:②④.
故答案为:②④.
| x2 |
| 4-t |
| y2 |
| t-1 |
①当4-t=t-1>0,即t=
| 5 |
| 2 |
②若曲线C为双曲线,则(4-t)(t-1)<0,解得t<1或t>4,正确;
③若4-t>0,t-1>0且4-t≠t-1,解得1<t<4且t≠
| 5 |
| 2 |
④若曲线C为焦点在x轴上的椭圆,则4-t>t-1>0,解得1<t<
| 5 |
| 2 |
综上可得真命题为:②④.
故答案为:②④.
点评:本题考查了分类讨论的思想方法,考查了椭圆双曲线圆的标准方程及其性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
双曲线
+
=1的焦距为( )
| x2 |
| a |
| y2 |
| a-1 |
| A、1 | ||
| B、2 | ||
C、2
| ||
D、2
|
若平面α⊥平面β,平面β⊥平面γ,则( )
| A、α∥γ |
| B、α⊥γ |
| C、α与γ相交但不垂直 |
| D、以上都有可能 |
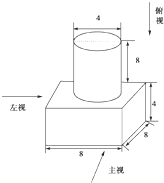 一几何体的直观图如图所示:
一几何体的直观图如图所示:


