题目内容
设a＞0，b＞0，c＞0，且a+b+c=1，证明不等式：
+
+
≥9．
| 1 |
| a |
| 1 |
| b |
| 1 |
| c |
考点：不等式的证明
专题：证明题
分析：依题意，可得
+
+
=
+
+
=3+（
+
）+（
+
）+（
+
），利用基本不等式即可证得结论
| 1 |
| a |
| 1 |
| b |
| 1 |
| c |
| a+b+c |
| a |
| a+b+c |
| b |
| a+b+c |
| c |
| b |
| a |
| a |
| b |
| c |
| a |
| a |
| c |
| c |
| b |
| b |
| c |
解答：
证明：∵a＞0，b＞0，c＞0，且a+b+c=1，
∴
+
+
=
+
+
=3+（
+
）+（
+
）+（
+
）
≥3+2
+2
+2
=3+2+2+2=9（当且仅当a=b=c时取“=”）（证毕）．
∴
| 1 |
| a |
| 1 |
| b |
| 1 |
| c |
| a+b+c |
| a |
| a+b+c |
| b |
| a+b+c |
| c |
=3+（
| b |
| a |
| a |
| b |
| c |
| a |
| a |
| c |
| c |
| b |
| b |
| c |
≥3+2
|
|
|
=3+2+2+2=9（当且仅当a=b=c时取“=”）（证毕）．
点评：本题考查不等式的证明，着重考查基本不等式的应用，注意等号成立的条件，考查推理论证能力，属于中档题．
练习册系列答案
相关题目
已知点（a，2）（a＞0）到直线l：x-y+3=0的距离为
，则a=（ ）
| 2 |
A、
| ||||
| B、1或-3 | ||||
C、
| ||||
D、
|
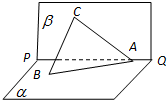已知直二面角α-PQ-β，A∈PQ，B∈α，C∈β，CA=CB，∠BAP=45°，直线CA和平面α所成的角为30°．