题目内容
分别求解下列关于x的不等式
(1)|x2-8x|≥12
(2)|x-3|+|x+5|≤14.
(1)|x2-8x|≥12
(2)|x-3|+|x+5|≤14.
考点:绝对值不等式的解法
专题:不等式的解法及应用
分析:(1)原不等式转化为:x2-8x≤-12或x2-8x≥12,分别解之即可;
(2)通过分x<-5,-5≤x≤3与当x>3三类讨论,去掉绝对值符号,分别解相应的不等式,最后取并即可.
(2)通过分x<-5,-5≤x≤3与当x>3三类讨论,去掉绝对值符号,分别解相应的不等式,最后取并即可.
解答:
分别求解下列不等式(12分)
(1)解:原不等式转化为:x2-8x≤-12或x2-8x≥12,
即:2≤x≤6或x≤4-
或x≥4+
,
∴原不等式的解集为{x|2≤x≤6或x≤4-
或x≥4+
};
(2)解:分步讨论如下:
①当x<-5时,原不等式转化为 3-x-x-5≤14⇒x≥-8,
即:-8≤x<-5;
②当-5≤x≤3时,原不等式可化为3-x+x+5≤14⇒8≤14,
即:-5≤x≤3,
③当x>3时,原不等式可化为x-3+x+5≤14⇒x≤6,
即:3<x≤6;
综合①②③可得原不等式的解集为:{x|-8≤x≤6}.
(1)解:原不等式转化为:x2-8x≤-12或x2-8x≥12,
即:2≤x≤6或x≤4-
| 7 |
| 7 |
∴原不等式的解集为{x|2≤x≤6或x≤4-
| 7 |
| 7 |
(2)解:分步讨论如下:
①当x<-5时,原不等式转化为 3-x-x-5≤14⇒x≥-8,
即:-8≤x<-5;
②当-5≤x≤3时,原不等式可化为3-x+x+5≤14⇒8≤14,
即:-5≤x≤3,
③当x>3时,原不等式可化为x-3+x+5≤14⇒x≤6,
即:3<x≤6;
综合①②③可得原不等式的解集为:{x|-8≤x≤6}.
点评:本题考查不等式的解法,着重考查绝对值不等式的解法,考查等价转化思想与分类讨论思想的综合应用,属于中档题.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
 如图所示:用篱笆围成一个一边靠墙的矩形菜园,假设墙有足够长.
如图所示:用篱笆围成一个一边靠墙的矩形菜园,假设墙有足够长. 2000辆汽车通过某一段公路时的时速的频率分布直方图如图所示.问:
2000辆汽车通过某一段公路时的时速的频率分布直方图如图所示.问: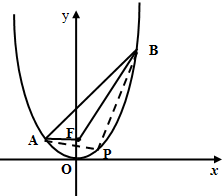 如图,已知抛物线x2=4y上两定点A,B分别在对称轴左、右两侧,F为抛物线的焦点,且|AF|=2,|BF|=5.
如图,已知抛物线x2=4y上两定点A,B分别在对称轴左、右两侧,F为抛物线的焦点,且|AF|=2,|BF|=5.