题目内容
函数f（x）=ax3-b的图象与直线y=3x+2相切于点A（1，f（1））．
（1）求a、b值；
（2）若函数f（x）在点B（-1，f（-1））的切线方程为l，直线m∥l，且m与抛物线y2=2x相切，求直线l和m的方程．
（1）求a、b值；
（2）若函数f（x）在点B（-1，f（-1））的切线方程为l，直线m∥l，且m与抛物线y2=2x相切，求直线l和m的方程．
考点：利用导数研究曲线上某点切线方程
专题：计算题,导数的概念及应用
分析：（1）求出f'（x）=3ax2，则f'（1）=3，求出切点，则f（1）=5，即可得到a，b；
（2）求出导数f'（x），得到切线l方程，设直线m的方程，代入抛物线方程，消去x，由判别式为0，即可得到l，m的方程．
（2）求出导数f'（x），得到切线l方程，设直线m的方程，代入抛物线方程，消去x，由判别式为0，即可得到l，m的方程．
解答：
解：（1）由已知得f'（x）=3ax2，则f'（1）=3a=3，∴a=1．
又点A在直线y=3x+2上，得f（1）=5，即A（1，5）．
代入f（x）=x3-b，得5=1-b，则b=-4．
（2）由f（x）=x3+4，得f'（x）=3x2，
∴k=f'（-1）=3，又B（-1，3）．
∴切线l方程为y-3=3（x+1），即3x-y+6=0．
设直线m的方程为y=3x+t，代人y2=2x得3y2-2y+2t=0．
∴△=4-24t=0，从而t=
．
所以直线m的方程为3x-y+
=0．
又点A在直线y=3x+2上，得f（1）=5，即A（1，5）．
代入f（x）=x3-b，得5=1-b，则b=-4．
（2）由f（x）=x3+4，得f'（x）=3x2，
∴k=f'（-1）=3，又B（-1，3）．
∴切线l方程为y-3=3（x+1），即3x-y+6=0．
设直线m的方程为y=3x+t，代人y2=2x得3y2-2y+2t=0．
∴△=4-24t=0，从而t=
| 1 |
| 6 |
所以直线m的方程为3x-y+
| 1 |
| 6 |
点评：本题考查导数的几何意义：曲线在该点处的切线的斜率，考查两直线的位置关系，直线与抛物线方程联立，消去一个未知数，运用判别式为0，解决相切问题，属于基础题．
练习册系列答案
相关题目
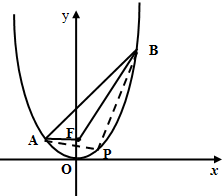如图，已知抛物线x2=4y上两定点A，B分别在对称轴左、右两侧，F为抛物线的焦点，且|AF|=2，|BF|=5．
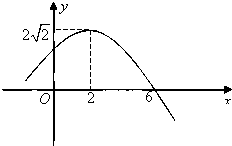已知函数y=Asin（ωx+φ），x∈R（其中A＞0，ω＞0，|φ|＜