题目内容
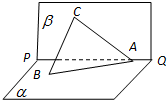 已知直二面角α-PQ-β,A∈PQ,B∈α,C∈β,CA=CB,∠BAP=45°,直线CA和平面α所成的角为30°.
已知直二面角α-PQ-β,A∈PQ,B∈α,C∈β,CA=CB,∠BAP=45°,直线CA和平面α所成的角为30°.(1)求证:BC⊥PQ;
(2)若AC=2,求二面角B-AC-P的正切值.
考点:二面角的平面角及求法,空间中直线与直线之间的位置关系
专题:空间角
分析:(1)在平面β内过点C作CO⊥PQ于点O,连接OB.利用面面垂直的性质可得:CO⊥α,由CA=CB,可得OA=OB.从而BO⊥PQ,利用线面垂直的判定可得PQ⊥平面OBC.再利用线面垂直的性质定理即可得出.
(2)由(1)知,BO⊥PQ,利用面面垂直的性质可得BO⊥β.过点O作OH⊥AC于点H,连接BH,由三垂线定理知,可得∠BHO是二面角B-AC-P的平面角.再利用直角三角形的边角关系即可得出.
(2)由(1)知,BO⊥PQ,利用面面垂直的性质可得BO⊥β.过点O作OH⊥AC于点H,连接BH,由三垂线定理知,可得∠BHO是二面角B-AC-P的平面角.再利用直角三角形的边角关系即可得出.
解答:
解:(1)在平面β内过点C作CO⊥PQ于点O,连接OB.
∵α⊥β,α∩β=PQ,
∴CO⊥α,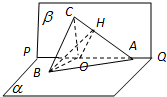
又∵CA=CB,∴OA=OB.
而∠BAO=45°,∴∠ABO=45°,∠AOB=90°,
从而BO⊥PQ,又BO∩OC=O,
∴PQ⊥平面OBC.
又BC?平面OBC,
故PQ⊥BC.
(2)由(1)知,BO⊥PQ,
又α⊥β,α∩β=PQ,BO?α,∴BO⊥β.
过点O作OH⊥AC于点H,连接BH,
由三垂线定理知,BH⊥AC.
故∠BHO是二面角B-AC-P的平面角.
由(1)知,CO⊥α,∴∠CAO是CA和平面α所成的角,则∠CAO=30°,
在Rt△AEM,则AO=
,OH=AOsin30°=
.
在Rt△OAB中,∠ABO=∠BAO=45°,∴BO=AO=
,
于是在Rt△BOH中,tan∠BHO=
=2.
故二面角B-AC-P的正切值为2.
∵α⊥β,α∩β=PQ,
∴CO⊥α,

又∵CA=CB,∴OA=OB.
而∠BAO=45°,∴∠ABO=45°,∠AOB=90°,
从而BO⊥PQ,又BO∩OC=O,
∴PQ⊥平面OBC.
又BC?平面OBC,
故PQ⊥BC.
(2)由(1)知,BO⊥PQ,
又α⊥β,α∩β=PQ,BO?α,∴BO⊥β.
过点O作OH⊥AC于点H,连接BH,
由三垂线定理知,BH⊥AC.
故∠BHO是二面角B-AC-P的平面角.
由(1)知,CO⊥α,∴∠CAO是CA和平面α所成的角,则∠CAO=30°,
在Rt△AEM,则AO=
| 3 |
| ||
| 2 |
在Rt△OAB中,∠ABO=∠BAO=45°,∴BO=AO=
| 3 |
于是在Rt△BOH中,tan∠BHO=
| BO |
| OH |
故二面角B-AC-P的正切值为2.
点评:本题考查了线面与面面垂直的判定与性质定理、三垂线定理、二面角、直角三角形的边角关系,考查了推理能力与计算能力,属于难题.

练习册系列答案
 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
|
|=1,|
|=2,
•(
-2
)=0,则|
-
|=( )
| a |
| b |
| a |
| a |
| b |
| a |
| b |
| A、2 | B、4 | C、1 | D、8 |
 2000辆汽车通过某一段公路时的时速的频率分布直方图如图所示.问:
2000辆汽车通过某一段公路时的时速的频率分布直方图如图所示.问: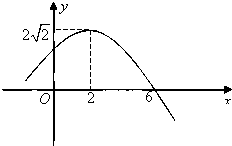 已知函数y=Asin(ωx+φ),x∈R(其中A>0,ω>0,|φ|<
已知函数y=Asin(ωx+φ),x∈R(其中A>0,ω>0,|φ|<