题目内容
已知函数y=3x，证明函数在x∈R上单调递增．
考点：函数单调性的判断与证明
专题：证明题,函数的性质及应用,导数的综合应用
分析：先求导，通过导数判断函数的单调性．
解答：
证明：∵y′=3x×ln3，
又∵ln3＞0，3x＞0，
∴y′＞0，
∴函数y=3x在R上单调递增．
又∵ln3＞0，3x＞0，
∴y′＞0，
∴函数y=3x在R上单调递增．
点评：本题考查了函数单调性的证明，一般有两种方法，定义法，导数法．
练习册系列答案
相关题目
已知命题“若p则￢q”是真命题，则下列命题中一定是真命题的为（ ）
| A、若￢p则q |
| B、若￢q则p |
| C、若q则￢p |
| D、若￢p则￢q |
如图所示：用篱笆围成一个一边靠墙的矩形菜园，假设墙有足够长．
如图，点A在直线x=5上移动，等腰△OPA的顶角∠OPA为120°（O，P，A按顺时针方向排列），求点P极坐标系的轨迹方程，并化成直角坐标系方程．
2000辆汽车通过某一段公路时的时速的频率分布直方图如图所示．问：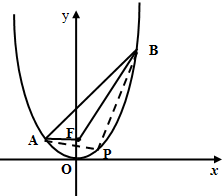
如图，已知抛物线x2=4y上两定点A，B分别在对称轴左、右两侧，F为抛物线的焦点，且|AF|=2，|BF|=5．