题目内容
已知关于x的二次函数f(x)=ax2-4bx+1,
(1)设集合P={-1,1,2,3,4,5}和Q={-2,-1,1,2,3,4,},分别从集合P和集合Q中任取一个数作为a和b的值,求函数y=f(x)在区间[1,+∞)上是增函数的概率;
(2)若a是从区间[1,3]任取的一个数,b是从区间[1,3]任取的一个数,求函数f(x)在区间[1,+∞)上是增函数的概率.
(1)设集合P={-1,1,2,3,4,5}和Q={-2,-1,1,2,3,4,},分别从集合P和集合Q中任取一个数作为a和b的值,求函数y=f(x)在区间[1,+∞)上是增函数的概率;
(2)若a是从区间[1,3]任取的一个数,b是从区间[1,3]任取的一个数,求函数f(x)在区间[1,+∞)上是增函数的概率.
考点:几何概型,古典概型及其概率计算公式
专题:概率与统计
分析:(1)求出方程f(x)=0有两相等实根的等价条件,利用古典概型的概率公式,即可得到结论.
(2)作出不等式组对应的平面区域,利用几何概型的概率公式求出相应的面积即可得到结论.
(2)作出不等式组对应的平面区域,利用几何概型的概率公式求出相应的面积即可得到结论.
解答:
解:(1)设集合P={-1,1,2,3,4,5}和Q={-2,-1,1,2,3,4,},分别从集合P和集合Q中任取一个数作为a和b的值,
则满足条件的a,b共有6×6=36种.
若a=-1,则函数y=f(x)在区间[1,+∞)上是增函数不成立,
若a>0,要使函数y=f(x)在区间[1,+∞)上是增函数,则对称轴x=-
=
≤1,即a≥2b,
①若a=1,则b=-2,-1;
②若a=2,则b=-2,-1,1;
③若a=3,则b=-2,-1,1;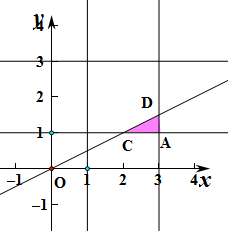
④若a=4,则b=-2,-1,1,2;
⑤若a=5,则b=-2,-1,1,2,
∴故满足条件的数对(a,b)共有16种,
则根据古典概型的概率公式可得函数y=f(x)在区间[1,+∞)上是增函数的概率P=
=
(2)∵a是从区间[1,3]任取的一个数,b是从区间[1,3]任取的一个数
∴1≤a≤3,且1≤b≤3对应区域的面积S=2×2=4,
∴若函数y=f(x)在区间[1,+∞)上是增函数,则对称轴x=-
=
≤1,即a≥2b,
作出不等式组对应的平面区域如图:阴影部分
则A(3,1),
当a=3时,b=
,即D(3,
),
当b=1时,a=2,即C(2,1),
则三角形ACD的面积S=
×(3-2)×(
-1)=
则由几何概型的概率公式可得函数y=f(x)在区间[1,+∞)上是增函数的概率为
=
.
则满足条件的a,b共有6×6=36种.
若a=-1,则函数y=f(x)在区间[1,+∞)上是增函数不成立,
若a>0,要使函数y=f(x)在区间[1,+∞)上是增函数,则对称轴x=-
| -4b |
| 2a |
| 2b |
| a |
①若a=1,则b=-2,-1;
②若a=2,则b=-2,-1,1;
③若a=3,则b=-2,-1,1;
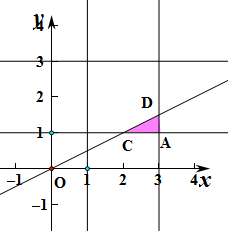
④若a=4,则b=-2,-1,1,2;
⑤若a=5,则b=-2,-1,1,2,
∴故满足条件的数对(a,b)共有16种,
则根据古典概型的概率公式可得函数y=f(x)在区间[1,+∞)上是增函数的概率P=
| 16 |
| 36 |
| 4 |
| 9 |
(2)∵a是从区间[1,3]任取的一个数,b是从区间[1,3]任取的一个数
∴1≤a≤3,且1≤b≤3对应区域的面积S=2×2=4,
∴若函数y=f(x)在区间[1,+∞)上是增函数,则对称轴x=-
| -4b |
| 2a |
| 2b |
| a |
作出不等式组对应的平面区域如图:阴影部分
则A(3,1),
当a=3时,b=
| 3 |
| 2 |
| 3 |
| 2 |
当b=1时,a=2,即C(2,1),
则三角形ACD的面积S=
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 4 |
则由几何概型的概率公式可得函数y=f(x)在区间[1,+∞)上是增函数的概率为
| ||
| 4 |
| 1 |
| 16 |
点评:本题主要考查概率的计算,根据古典关系和几何概型的概率公式是解决本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目