题目内容
平面内给定三个向量
=(3,2),
=(-1,2),
=(4,1).
(1)若(
+k
)⊥(2
-
),求实数k;
(2)若向量
满足
∥
,且|
|=
,求向量
.
| a |
| b |
| c |
(1)若(
| a |
| c |
| b |
| a |
(2)若向量
| d |
| d |
| c |
| d |
| 34 |
| d |
考点:平面向量共线(平行)的坐标表示,平面向量数量积的运算
专题:平面向量及应用
分析:(1)由向量
=(3,2),
=(-1,2),
=(4,1),可得:
+k
=(4k+3,k+2),2
-
=(-5,2),进而根据(
+k
)⊥(2
-
),可得-5(4k+3)+2(k+2)=0,解得实数k的值;
(2)由向量
满足
∥
,
=(4,1).可设
=(4x,x),结合|
|=
,可得17x2=34,进而可得向量
的坐标.
| a |
| b |
| c |
| a |
| c |
| b |
| a |
| a |
| c |
| b |
| a |
(2)由向量
| d |
| d |
| c |
| c |
| d |
| d |
| 34 |
| d |
解答:
解:(1)∵向量
=(3,2),
=(-1,2),
=(4,1),
∴
+k
=(4k+3,k+2),2
-
=(-5,2),
∵(
+k
)⊥(2
-
),
∴-5(4k+3)+2(k+2)=0,
即18k+11=0,
解得:k=-
,
(2)∵向量
满足
∥
,
=(4,1).
设
=(4x,x),
又∵|
|=
,
∴17x2=34,
解得:x=±
,
∴
=(4
,
)或
=(-4
,-
)
| a |
| b |
| c |
∴
| a |
| c |
| b |
| a |
∵(
| a |
| c |
| b |
| a |
∴-5(4k+3)+2(k+2)=0,
即18k+11=0,
解得:k=-
| 11 |
| 18 |
(2)∵向量
| d |
| d |
| c |
| c |
设
| d |
又∵|
| d |
| 34 |
∴17x2=34,
解得:x=±
| 2 |
∴
| d |
| 2 |
| 2 |
| d |
| 2 |
| 2 |
点评:本题考查的知识点是平面向量共线(平行)的坐标表示,平面向量垂直的充要条件,是向量简单综合应用,难度不大,属于基础题.

练习册系列答案
相关题目
曲线y=
x3+x在点(1,
)处的切线与坐标轴围成的三角形的面积为( )
| 1 |
| 3 |
| 4 |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|

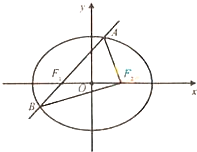 如图,椭圆E:
如图,椭圆E: