题目内容
设x,y为正数,且x+y=1,用反证法证明:(
-1)(
-1)≥9.
| 1 |
| x2 |
| 1 |
| y2 |
考点:反证法与放缩法
专题:推理和证明
分析:直接利用反证法的证明步骤,反设所证明的不等式,推出错误结论(2x-1)2<0,即可证明原不等式成立.
解答:
证明:假设(
-1)(
-1)<9,由于x,y>0,且x+y=1,所以(
-1)(
-1)=
×
=
×
=
×
=
×
<9,
由此得(2x-1)2<0,这是不可能的.
故原不等式成立.
| 1 |
| x2 |
| 1 |
| y2 |
| 1 |
| x2 |
| 1 |
| y2 |
| (1+x)(1-x) |
| x2 |
| (1+y)(1-y) |
| y2 |
| (1+x)y |
| x2 |
| (1+y)x |
| y2 |
| 1+x |
| x |
| 1+y |
| y |
=
| 1+x |
| x |
| 2-x |
| 1-x |
由此得(2x-1)2<0,这是不可能的.
故原不等式成立.
点评:本题考查不等式的证明,反证法的应用,注意:正确推理过程得到错误结论是解题的关键.

练习册系列答案
相关题目
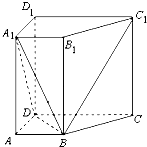 如图,已知在直四棱柱ABCD-A1B1C1D1(侧棱垂直底面的棱柱)中,AD⊥DC,AB∥DC,DC=DD1=2AD=2AB=2.
如图,已知在直四棱柱ABCD-A1B1C1D1(侧棱垂直底面的棱柱)中,AD⊥DC,AB∥DC,DC=DD1=2AD=2AB=2.