题目内容
曲线y=
x3+x在点(1,
)处的切线与坐标轴围成的三角形的面积为( )
| 1 |
| 3 |
| 4 |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:利用导数研究曲线上某点切线方程
专题:计算题,导数的概念及应用
分析:先对函数求导,然后根据导数的几何意义求出曲线在点(1,
)处的切线斜率,进而求出切线方程,再分别求出与x,y轴的交点,由三角形的面积公式即可得到.
| 4 |
| 3 |
解答:
解:∵y′=x2+1,
∴曲线y=
x3+x在点(1,
)处的切线斜率k=f′(1)=2,
∴所求的切线方程为y-
=2(x-1)即2x-y-
=0
令x=0可得y=-
,令y=0可得x=
,
则与两坐标轴围成三角形的面积是S=
×
×
=
.
故选B.
∴曲线y=
| 1 |
| 3 |
| 4 |
| 3 |
∴所求的切线方程为y-
| 4 |
| 3 |
| 2 |
| 3 |
令x=0可得y=-
| 2 |
| 3 |
| 1 |
| 3 |
则与两坐标轴围成三角形的面积是S=
| 1 |
| 2 |
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 9 |
故选B.
点评:本题主要考查了导数的几何意义的应用及曲线在一点处的切线方程的求解,考查运算能力,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
下列说法正确的是( )
| A、命题“?x0∈R,x02+x0+1<0”的否定是:“?x∈R,x2+x+1>0” |
| B、“x=-1”是“x2-5x-6=0”的必要不充分条件 |
| C、命题“若x2=1,则x=1”的否命题是:若x2=1,则x≠1 |
| D、命题“若x=y,则sin x=sin y”的逆否命题为真命题 |
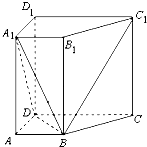 如图,已知在直四棱柱ABCD-A1B1C1D1(侧棱垂直底面的棱柱)中,AD⊥DC,AB∥DC,DC=DD1=2AD=2AB=2.
如图,已知在直四棱柱ABCD-A1B1C1D1(侧棱垂直底面的棱柱)中,AD⊥DC,AB∥DC,DC=DD1=2AD=2AB=2.