题目内容
函数y=-cos(
-
)的单调递增区间是( )
| π |
| 3 |
| x |
| 2 |
A、[2kπ-
| ||||
B、[4kπ-
| ||||
C、[2kπ+
| ||||
D、[4kπ+
|
考点:余弦函数的图象
专题:三角函数的图像与性质
分析:先利用诱导公式化简函数的解析式为y=cos(
-
),再根据余弦函数的单调性求出它的单调区间.
| x |
| 2 |
| 4π |
| 3 |
解答:
解:函数y=-cos(
-
)=cos(π+
-
)=cos(
-
),
令 2kπ-π≤
-
≤2kπ,k∈z,求得4kπ+
≤x≤4kπ+
,k∈z,
故函数的单调递增区间为[4kπ+
π,4kπ+
π],k∈z,
故选:D.
| π |
| 3 |
| x |
| 2 |
| π |
| 3 |
| x |
| 2 |
| x |
| 2 |
| 4π |
| 3 |
令 2kπ-π≤
| x |
| 2 |
| 4π |
| 3 |
| 2π |
| 3 |
| 8π |
| 3 |
故函数的单调递增区间为[4kπ+
| 2 |
| 3 |
| 8 |
| 3 |
故选:D.
点评:本题主要考查以及诱导公式的应用,余弦函数的单调性,属于基础题.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案
相关题目
下列关于正弦定理的叙述或变形中错误的是( )
| A、在△ABC中,a:b:c=sinA:sinB:sinC | ||||
| B、在△ABC中,a=b?sin2A=sin2B | ||||
C、△ABC中:
| ||||
| D、△ABC中,正弦值较大的角所对的边也较大 |
已知随机变量X~N(4,1),且P(3≤X≤5)=0.6826,则P(X<3)等于( )
| A、0.1585 |
| B、0.1586 |
| C、0.1587 |
| D、0.1588 |
点A(4,3),又P为抛物线x2=4y上一动点,则P到A的距离与P到x轴距离之和的最小值( )
| A、5 | ||
| B、4 | ||
C、2
| ||
D、2
|
已知Rt△ABC中,∠C=90°,AB=5,BC=4,以BC为直径的圆交AB于D,则BD的长为( )
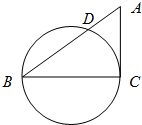

| A、4 | ||
B、
| ||
C、
| ||
D、
|
函数f(x)=x2+bx在点A(1,f(1))处的切线方程为3x-y-1=0,设数列{
}的前n项和Sn,则S2011为( )
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|