题目内容
设f(x)=3x,且f(a+2)=18,g(x)=3ax-4x(x∈R).
(1)求g(x)的解析式;
(2)判断g(x)在[0,1]上的单调性并用定义证明;
(3)设M={m|方程g(t)-m=0在[-2,2]上有两个不同的解},求集合M.
(1)求g(x)的解析式;
(2)判断g(x)在[0,1]上的单调性并用定义证明;
(3)设M={m|方程g(t)-m=0在[-2,2]上有两个不同的解},求集合M.
考点:利用导数研究函数的单调性,根的存在性及根的个数判断
专题:计算题,作图题,证明题,导数的综合应用
分析:(1)由题意得3a+2=18,从而可得3a=2;从而可得g(x)=3ax-4x=2x-4x,
(2)先判断,后证明,用定义法证明单调性一般可以分为五步,取值,作差,化简变形,判号,下结论;
(3)方程可化为2t-4t-m=0,令k=2t,t∈[-2,2],则k∈[
,4];从而可得m=k-k2=-(k-
)2+
;从而求集合M.
(2)先判断,后证明,用定义法证明单调性一般可以分为五步,取值,作差,化简变形,判号,下结论;
(3)方程可化为2t-4t-m=0,令k=2t,t∈[-2,2],则k∈[
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
解答:
 解:(1)∵f(x)=3x,且f(a+2)=18;
解:(1)∵f(x)=3x,且f(a+2)=18;
∴3a+2=18,3a=2;
∴g(x)=3ax-4x=2x-4x,
(2)g(x)在[0,1]上单调递减,证明如下:
设0≤x1≤x2≤1,
g(x2)-g(x1)=2x2-4x2-2x1+4x1
=(2x2-2x1)(1-2x1-2x2);
∵0≤x1≤x2≤1,
∴2x2>2x1,1-2x1-2x2<0;
∴(2x2-2x1)(1-2x1-2x2)<0;
∴g(x2)-g(x1)<0,
∴g(x)在[0,1]上单调递减;
(3)方程可化为2t-4t-m=0,
令k=2t,t∈[-2,2],则k∈[
,4];
则方程k-k2-m=0在[
,4]内有两个不同的解;
m=k-k2=-(k-
)2+
;
由图知m∈[
,
)时,方程有两个不同解;
故M=[
,
).
 解:(1)∵f(x)=3x,且f(a+2)=18;
解:(1)∵f(x)=3x,且f(a+2)=18;∴3a+2=18,3a=2;
∴g(x)=3ax-4x=2x-4x,
(2)g(x)在[0,1]上单调递减,证明如下:
设0≤x1≤x2≤1,
g(x2)-g(x1)=2x2-4x2-2x1+4x1
=(2x2-2x1)(1-2x1-2x2);
∵0≤x1≤x2≤1,
∴2x2>2x1,1-2x1-2x2<0;
∴(2x2-2x1)(1-2x1-2x2)<0;
∴g(x2)-g(x1)<0,
∴g(x)在[0,1]上单调递减;
(3)方程可化为2t-4t-m=0,
令k=2t,t∈[-2,2],则k∈[
| 1 |
| 4 |
则方程k-k2-m=0在[
| 1 |
| 4 |
m=k-k2=-(k-
| 1 |
| 2 |
| 1 |
| 4 |
由图知m∈[
| 3 |
| 16 |
| 1 |
| 4 |
故M=[
| 3 |
| 16 |
| 1 |
| 4 |
点评:本题考查了导数的综合应用及换元法的应用,同时考查了方程的根与函数的关系,属于中档题.

练习册系列答案
相关题目
下面两个程序最后输出的“sum”应分别等于( )


| A、都是17 | B、都是21 |
| C、21和17 | D、14和21 |
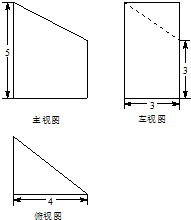
某几何体的三视图如图所示,则该几何体的体积为( )

| A、26 | ||
B、42+3
| ||
| C、62 | ||
D、42-3
|