题目内容
1.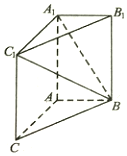 如图,在三棱柱ABC-A1B1C1中,平面ABC⊥平面AA1B1B,四边形AA1B1B是矩形,且AB=1,AC=2,BC=$\sqrt{5}$.
如图,在三棱柱ABC-A1B1C1中,平面ABC⊥平面AA1B1B,四边形AA1B1B是矩形,且AB=1,AC=2,BC=$\sqrt{5}$.(1)求证:AA1⊥平面ABC;
(2)若直线BC1与平面ABC所成角的正弦值为$\frac{2}{3}$,求二面角A1-BC1-B1的余弦值.
分析 (1)推导出AA1⊥AB,由此能证明AA1⊥平面ABC.
(2)以A为原点建立空间直角坐标系A-xyz,利用向量法能求出二面角A1-BC1-B1的余弦值.
解答 证明:(1)∵三棱柱ABC-A1B1C1中,四边形AA1B1B是矩形,
∴AA1⊥AB,
∵平面ABC⊥平面AA1B1B,且AA1垂直于这两个平面的交线AB,
∴AA1⊥平面ABC.
解:(2)由(1)知AA1⊥AB,AA1⊥AC,
∵AB=1,AC=2,BC=$\sqrt{5}$,∴AB2+AC2=BC2,∴AB⊥AC,
如图,以A为原点建立空间直角坐标系A-xyz,
由(1)知CC1⊥平面ABC,
∴直线BC1与平面ABC所成角的大小即为∠C1BC的大小,
由已知得tan$∠{C}_{1}BC=\frac{2}{\sqrt{5}}$,
∴CC1=2,则C1(2,0,2),B(0,1,0),B1(0,1,2),A1(0,0,2),
$\overrightarrow{B{A}_{1}}$=(0,-1,2),$\overrightarrow{B{C}_{1}}$=(2,-1,2),
设平面A1BC1的法向量$\overrightarrow{n}$=(x,y,z),
则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{B{A}_{1}}=-y+2z=0}\\{\overrightarrow{n}•\overrightarrow{B{C}_{1}}=2x-y+2z=0}\end{array}\right.$,取z=1,得$\overrightarrow{n}$=(0,2,1),
同理求得平面BB1C1的法向量$\overrightarrow{m}$=(1,2,0),
∴cos<$\overrightarrow{m},\overrightarrow{n}$>=$\frac{\overrightarrow{m}•\overrightarrow{n}}{|\overrightarrow{m}|•|\overrightarrow{n}|}$=$\frac{4}{5}$,
由图知二面角A1-BC1-B1的平面角为锐角,
∴二面角A1-BC1-B1的余弦值为$\frac{4}{5}$.
点评 本题考查线面垂直的证明,考查二面角的余弦值的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案| A. | $\frac{1}{3}$ | B. | $-\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $-\frac{1}{2}$ |
| A. | f(x)在$({0,\frac{π}{2}})$单调递减 | B. | f(x)在$({\frac{π}{2},π})$单调递减 | ||
| C. | f(x)在$({0,\frac{π}{2}})$单调递增 | D. | f(x)在(0,π)单调递增 |
| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
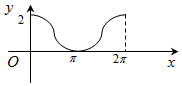
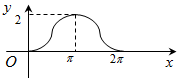
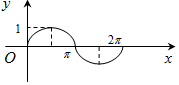
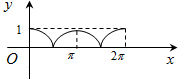
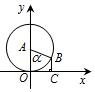 如图,圆A的半径为1,且A点的坐标为(0,1),B为圆上的动点,角α的始边为射线AO,终边为射线AB,过点B作x轴的垂线,垂足为C,将BC表示成α的函数f(α),则y=f(α)在[0,2π]的在图象大致为( )
如图,圆A的半径为1,且A点的坐标为(0,1),B为圆上的动点,角α的始边为射线AO,终边为射线AB,过点B作x轴的垂线,垂足为C,将BC表示成α的函数f(α),则y=f(α)在[0,2π]的在图象大致为( )