题目内容
6．
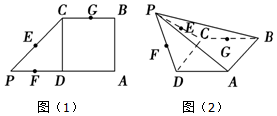在如图（1）的平面图形中，ABCD为正方形，CDP为等腰直角三角形，E、F、G分别是PC、PD、CB的中点，将△PCD沿CD折起，得到四棱锥P-ABCD如图（2）．求证：在四棱锥P-ABCD中，AP∥平面EFG．
分析 连接E、F，连接E、G，可得EF∥平面PAB．EG∥平面PAB．即可证平面PAB∥平面EFG
解答 
证明：连接E、F，连接E、G，在四棱锥PABCD中，E，F分别为PC，PD的中点，
∴EF∥CD．∵AB∥CD，∴EF∥AB．
∵EF?平面PAB，AB?平面PAB，∴EF∥平面PAB．
同理EG∥平面PAB．又EF∩EG=E，
∴平面PAB∥平面EFG．又AP?平面PAB，
∴AP∥平面EFG．
点评 本题考查了空间线面平行的判定，属于中档题．
练习册系列答案
相关题目
16．设非零向量$\overrightarrow{a}$=（x，2x），$\overrightarrow{b}$=（-3x，2），且$\overrightarrow{a}$，$\overrightarrow{b}$的夹角为钝角，则x的取值范围是（ ）
| A． | （-∞，0） | B． | （$\frac{4}{3}$，0） | ||
| C． | （-∞，0）∪（$\frac{4}{3}$，0） | D． | （-∞，-$\frac{1}{3}$）∪（-$\frac{1}{3}$，0）∪（$\frac{4}{3}$，+∞） |
14．已知函数f（x）=$\sqrt{3}$sin（ωx+φ）（ω＞0，-$\frac{π}{2}$≤φ＜$\frac{π}{2}$）的图象关于直线x=$\frac{π}{3}$对称，且图象上相邻最高点的距离为π．将函数y=f（x）的图象向右平移$\frac{π}{12}$个单位后，得到y=g（x）的图象，则g（x）的单调递减区间为．
| A． | [kπ+$\frac{5π}{12}$，kπ+$\frac{11π}{12}$]，k∈Z | B． | [kπ-$\frac{5π}{12}$，kπ-$\frac{11π}{12}$]，k∈Z | ||
| C． | [kπ-$\frac{5π}{12}$，kπ+$\frac{11π}{12}$]，k∈Z | D． | [kπ+$\frac{5π}{12}$，kπ-$\frac{11π}{12}$]，k∈Z |
1．已知O为直角坐标系原点，P，Q的坐标满足不等式组$\left\{\begin{array}{l}4x+3y-25≤0\\ x-2y+2≤0\\ x-1≥0\end{array}\right.$，则cos∠POQ的最小值为（ ）
| A． | $\frac{{\sqrt{2}}}{2}$ | B． | $\frac{{\sqrt{3}}}{2}$ | C． | $\frac{1}{2}$ | D． | 0 |