题目内容
11.设$\overrightarrow{a}$=(cosx,-1),$\overrightarrow{b}$=(sinx-cosx,-1),函数f(x)=$\overrightarrow{a}$•$\overrightarrow{b}$-$\frac{1}{2}$(1)求函数f(x)的解析式;
(2)求函数f(x)的对称轴方程和对称中心的坐标;
(3)求不等式f(x)≥$\frac{1}{2}$的解集.
分析 (1)根据向量的数量积和二倍角公式以及两角差的正弦公式即可求出f(x)的解析式,
(2)根据称轴方程和对称中心的坐标的定义即可求出,
(3)根据正弦函数的图象和性质即可求出
解答 解:(1)$\overrightarrow{a}$=(cosx,-1),$\overrightarrow{b}$=(sinx-cosx,-1),
∴函数f(x)=$\overrightarrow{a}$•$\overrightarrow{b}$-$\frac{1}{2}$=cosx(sinx-cosx)+1-$\frac{1}{2}$=cosxsinx-cos2x+$\frac{1}{2}$=$\frac{1}{2}$sin2x-$\frac{1}{2}$cos2x-$\frac{1}{2}$+$\frac{1}{2}$=$\frac{\sqrt{2}}{2}$sin(2x-$\frac{π}{4}$),
(2)令2x-$\frac{π}{4}$=kπ+$\frac{π}{2}$,即x=$\frac{kπ}{2}$+$\frac{3}{8}$π,k∈Z,
对称轴方程为:x=$\frac{kπ}{2}$+$\frac{3}{8}$π,k∈Z,
令2x-$\frac{π}{4}$=kπ,即x=$\frac{kπ}{2}$+$\frac{1}{8}$π,k∈Z,
∴对称中心为($\frac{kπ}{2}$+$\frac{1}{8}$π,0)k∈Z,
(3)∵f(x)≥$\frac{1}{2}$,
∴$\frac{\sqrt{2}}{2}$sin(2x-$\frac{π}{4}$)≥$\frac{1}{2}$
即sin(2x-$\frac{π}{4}$)≥$\frac{\sqrt{2}}{2}$,
∴$\frac{π}{4}$+2kπ≤2x-$\frac{π}{4}$≤$\frac{3π}{4}$+2kπ,
∴$\frac{π}{4}$+kπ≤x≤$\frac{π}{2}$+kπ,
∴不等式f(x)≥$\frac{1}{2}$的解集为[$\frac{π}{4}$+kπ,$\frac{π}{2}$+kπ],k∈Z.
点评 本题考查了向量的数量积的运算和三角函数的化简,以及正弦函数的有关性质,属于基础题

 一线名师权威作业本系列答案
一线名师权威作业本系列答案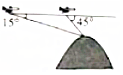 航空测量组的飞机航线和山顶在同一铅直平面内,已知飞机的高度为海拔10千米,速度为180千米/小时,飞机先看到山顶的俯角为15°,经过420秒后又看到山顶的俯角为45°,则山顶的海拔高度为(取$\sqrt{2}=1.4$,$\sqrt{3}=1.7$)( )
航空测量组的飞机航线和山顶在同一铅直平面内,已知飞机的高度为海拔10千米,速度为180千米/小时,飞机先看到山顶的俯角为15°,经过420秒后又看到山顶的俯角为45°,则山顶的海拔高度为(取$\sqrt{2}=1.4$,$\sqrt{3}=1.7$)( )| A. | 2.65千米 | B. | 7.35千米 | C. | 10千米 | D. | 10.5千米 |
| A. | 1 | B. | $\frac{64}{15}$ | C. | $\frac{16}{19}$ | D. | $\frac{1}{2}$ |
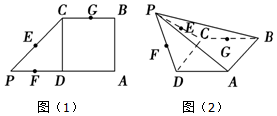 在如图(1)的平面图形中,ABCD为正方形,CDP为等腰直角三角形,E、F、G分别是PC、PD、CB的中点,将△PCD沿CD折起,得到四棱锥P-ABCD如图(2).
在如图(1)的平面图形中,ABCD为正方形,CDP为等腰直角三角形,E、F、G分别是PC、PD、CB的中点,将△PCD沿CD折起,得到四棱锥P-ABCD如图(2).