Question

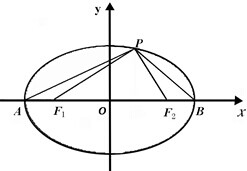如图，已知椭圆C：

x2

a2

+

y2

b2

=1（a＞b＞0）的离心率为

4

5

，左、右焦点分别为F₁和F₂，椭圆C与x轴的两交点分别为A、B，点P是椭圆上一点（不与点A、B重合），∠F₁PF₂=2β．
（1）若β=45°，三角形F₁PF₂的面积为36，求椭圆C的方程；
（2）在条件（1）下，过点Q（0，10）的直线l与椭圆C交于M，N两点，且|MN|=

90 2

17

，求l的方程及tan∠AMB．

Answer 1

考点：直线与圆锥曲线的关系,椭圆的标准方程

专题：计算题,圆锥曲线的定义、性质与方程

分析：（1）由题意三角形F₁PF₂为直角三角形，所以|PF₁|²+|PF₂|²=|F₁F₂|²，即（|PF₁|+|PF₂|）²-2|PF₁||PF₂|=
|F₁F₂|²，结合三角形F₁PF₂的面积为36，可求得b²=36，利用椭圆C的离心率为

4

5

，可得a²=100，从而可求椭圆C的方程；
（2）设直线l：y=kx+10，代入椭圆方程9x²+25y²-900=0，得（9+25k²）x²+500kx+1600=0，运用韦达定理和判别式大于0，以及弦长公式，解方程即可得到k²=1，进而求得M，N的坐标，求出直线BM的斜率，再由到角公式，即可得到tan∠AMB．

解答： 解：（1）∵∠F₁PF₂=2β=90°
∴三角形F₁PF₂为直角三角形，
∴|PF₁|²+|PF₂|²=|F₁F₂|²，
∴（|PF₁|+|PF₂|）²-2|PF₁||PF₂|=|F₁F₂|²，
∵三角形F₁PF₂的面积为36，
∴

1

2

|PF₁||PF₂|=36，∴|PF₁||PF₂|=72
∴（2a）²-2×72=（2c）²，∴b²=36，
∵椭圆C的离心率为

4

5

，
则

c2

a2

=

16

25

，即

a2-b2

a2

=

16

25

，∴a²=100，
∴椭圆C的方程为

x2

100

+

y2

36

=1．
（2）设直线l：y=kx+10，代入椭圆方程9x²+25y²-900=0，
得（9+25k²）x²+500kx+1600=0，
设M（x₁，y₁），N（x₂，y₂），则△=（500k）²-4×1600（9+25k²）＞0，
x₁+x₂=-

500k

9+25k2

，x₁x₂=

1600

9+25k2

，
则|MN|=

1+k2

|x₁-x₂|=

1+k2

•

( -500k 9+25k2 )2- 6400 9+25k2

=

90 2

17

，
即有9（9+25k²）²=289（1+k²）（50k²-32），即8825k⁴+1152k²-9977=0，
解得k²=1，或-

9977

8825

（舍去），检验得△＞0，则k=±1．
则直线l的方程为：y=±x+10；
若k=1，则有34x²+500x+1600=0，解得x₁=-

80

17

，x₂=-10．
即有M（-

80

17

，

90

17

），A（-10，0），B（10，0），
由于k_AM=1，k_BM=-

9

25

，
则tan∠AMB=

- 9 25 -1

1+(- 9 25 )×1

=-

17

8

．
若k=-1，同样有tan∠AMB=-

17

8

．
故l的方程为y=x+10或y=-x+10，tan∠AMB=-

17

8

．

点评：本题以椭圆的性质为载体，考查椭圆的标准方程，考查焦点三角形的面积计算，考查勾股定理的运用，考查直线方程和椭圆方程联立，消去未知数，得到x的方程，运用韦达定理，注意判别式大于0，以及弦长公式，和到角公式，考查运算能力，属于中档题．