题目内容
求下列函数的值域:
(1)y=2x+1,x∈{1,2,3,4,5};
(2)y=
+1;
(3)y=
;
(4)y=-x2-2x+3(-1≤x≤2).
(1)y=2x+1,x∈{1,2,3,4,5};
(2)y=
| x |
(3)y=
| 1-x2 |
| 1+x2 |
(4)y=-x2-2x+3(-1≤x≤2).
考点:函数的值域
专题:函数的性质及应用
分析:(1)y=2x+1,x∈{1,2,3,4,5},可得y∈{3,5,7,9,11};
(2)y=
+1≥1,由于
≥0,即可得出;
(3)变形y=
=
-1,由于x2≥0,可得0<
≤2,即可得出;
(4)y=-x2-2x+3=-(x+1)2+4,函数f(x)在[-1,2]上单调递减,可得f(2)≤f(x)≤f(-1).
(2)y=
| x |
| x |
(3)变形y=
| 1-x2 |
| 1+x2 |
| 2 |
| 1+x2 |
| 2 |
| 1+x2 |
(4)y=-x2-2x+3=-(x+1)2+4,函数f(x)在[-1,2]上单调递减,可得f(2)≤f(x)≤f(-1).
解答:
解:(1)y=2x+1,x∈{1,2,3,4,5},∴y∈{3,5,7,9,11};
(2)y=
+1≥1,其值域为[1,+∞);
(3)y=
=
-1,∵x2≥0,∴0<
≤2,∴-1<y≤1,函数的值域为(-1,1];
(4)y=-x2-2x+3=-(x+1)2+4,
函数f(x)在[-1,2]上单调递减,∴f(2)≤f(x)≤f(-1),即-5≤f(x)≤4,∴函数f(x)的值域为[-5,4].
(2)y=
| x |
(3)y=
| 1-x2 |
| 1+x2 |
| 2 |
| 1+x2 |
| 2 |
| 1+x2 |
(4)y=-x2-2x+3=-(x+1)2+4,
函数f(x)在[-1,2]上单调递减,∴f(2)≤f(x)≤f(-1),即-5≤f(x)≤4,∴函数f(x)的值域为[-5,4].
点评:本题考查了一次函数、二次函数、反比例函数、根式函数的单调性及函数的值域,考查了计算能力,属于基础题.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
函数y=sin|x|的图象是( )
A、 |
B、 |
C、 |
D、 |
已知
=(sinx,1,cox),
=(-1,sinx,cox)则
+
与
-
的夹角为( )
| a |
| b |
| a |
| b |
| a |
| b |
A、
| ||
B、
| ||
C、
| ||
D、
|
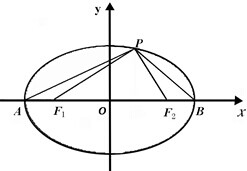 如图,已知椭圆C:
如图,已知椭圆C: