题目内容
△ABC中，若（
+
）•（
+
）=0，则△ABC为（ ）
| CA |
| CB |
| AC |
| CB |
| A、正三角形 | B、等腰三角形 |
| C、直角三角形 | D、无法确定 |
考点：平面向量数量积的运算
专题：平面向量及应用
分析：作△ABC的中线CD，则根据向量加法的平行四边形法则及题中条件得：2
•
=0，所以CD⊥AB，所以△ABC为等腰三角形．
| CD |
| AB |
解答：
解：如图，取AB边的中点D，连接CD，则：(
+
)•(
+
)=2
•
=0；
∴CD⊥AB；
∴CA=CB，∴△ABC为等腰三角形．
故选B．
解：如图，取AB边的中点D，连接CD，则：(| CA |
| CB |
| AC |
| CB |
| CD |
| AB |
∴CD⊥AB；
∴CA=CB，∴△ABC为等腰三角形．
故选B．
点评：考查中线向量，向量加法的平行四边形法则，向量的加法，两向量的数量积为0的充要条件．
练习册系列答案
名校课堂系列答案
相关题目
若1+2i是关于x的实系数方程x2+bx+c=0的一个复数根，则（ ）
| A、b=2，c=3 |
| B、b=-2，c=5 |
| C、b=-2，c=-1 |
| D、b=2，c=-1 |
若集合M={a，b，c}则有（ ）
| A、{a}∈M | B、c∈M |
| C、b?M | D、c={c} |
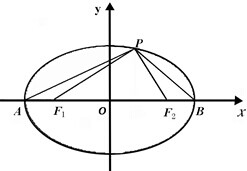如图，已知椭圆C：