题目内容
火车站A北偏东30°方向的C处有一电视塔，火车站正东方向的B处有一小汽车，测得BC距离为31km，该小汽车从B处以60公里每小时的速度前往火车站，20分钟后到达D处，测得离电视塔21km，问小汽车到火车站还需多长时间？
考点：解三角形的实际应用
专题：应用题,解三角形
分析：先画出图形，在△BCD中，求出sinβ，利用sinα=sin（β-60°），求出sinα，在△ADC中，由正弦定理，得AD，即可求出小汽车到火车站的时间．
解答：
解：由条件∠A=60°，设∠ACD=α，∠CDB=β，
在△BCD中，由余弦定理得cosβ=
=-
------------（4分）
∴sinβ=
．
∴sinα=sin（β-60°）=sinβcos60°-cosβsin60°=
．-----（8分）
在△ADC中，由正弦定理，得AD=
=15（km）-------（10分）
∴
×60=15（分钟）
答：到火车站还需15分钟．-------（12分）
解：由条件∠A=60°，设∠ACD=α，∠CDB=β，在△BCD中，由余弦定理得cosβ=
| CD2+BD2-BC2 |
| 2CD•BD |
| 1 |
| 7 |
∴sinβ=
4
| ||
| 7 |
∴sinα=sin（β-60°）=sinβcos60°-cosβsin60°=
5
| ||
| 14 |
在△ADC中，由正弦定理，得AD=
| CDsinα |
| sinA |
∴
| 15 |
| 60 |
答：到火车站还需15分钟．-------（12分）
点评：本题考查利用数学知识解决实际问题，考查正弦、余弦定理的运用，考查学生的计算能力，属于中档题．
练习册系列答案
相关题目
下列各函数值，其中符号为负的是（ ）
| A、sin（-1000°） | ||||||
| B、cos（-2200°） | ||||||
| C、tan（-10） | ||||||
D、
|
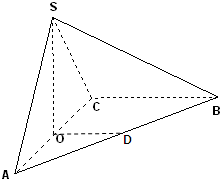在三棱锥S-ABC中，平面SAC⊥平面ABC，且△SAC是正三角形，O是AC的中点，D是AB的中点．