题目内容
(1)设n为不小于3的正整数,公差为1的等差数列a1,a2,…,an和首项为1的等比数列b1,b2,…,bn满足b1<a1<b2<a2<…<bn<an,求正整数n的最大值;
(2)对任意给定的不小于3的正整数n,证明:存在正整数x,使得等差数列{an}:xn+xn-1-1,xn+2xn-1-1,…,xn+nxn-1-1和等比数列{bn}:xn,(1+x)xn-1,…,x(1+x)n-1满足b1<a1<b2<a2<…<bn<an.
(2)对任意给定的不小于3的正整数n,证明:存在正整数x,使得等差数列{an}:xn+xn-1-1,xn+2xn-1-1,…,xn+nxn-1-1和等比数列{bn}:xn,(1+x)xn-1,…,x(1+x)n-1满足b1<a1<b2<a2<…<bn<an.
考点:等比数列的性质,等差数列的性质
专题:等差数列与等比数列
分析:(1)由已知及等差与等比数列的通项公式可得1<a1<b2<a1+1<b22<a1+2<b23<a1+3<b24<…,求解b2的范围即可求解n
(2)先表示出am=xn+xn-1-1+(m-1)•xn-1,bm=xn(1+
)m-1,结合已知不等关系可证明
(2)先表示出am=xn+xn-1-1+(m-1)•xn-1,bm=xn(1+
| 1 |
| x |
解答:
解:(1)由已知可得,an=a1+n-1,bn=b2n-1,1<b2(+
)
依题意有1<a1<b2<a1+1<b22<a1+2<b23<a1+3<b24<…(2分)
从而1<b2<2<b22<3<b23<4<…
即1<b2<2①,
<b2<
②,
<b2<
③,
<b2<
④,
<b2<
⑤,…,
由①②③④得,
<b2<
;因
<
,所以由①②③④⑤得,b2不存在了,从而正整数n的最大值为5; …(6分)
(2)依题意,am=xn+xn-1-1+(m-1)•xn-1,bm=xn(1+
)m-1,且m=1,2,…,n,
一方面,当x∈N*时,an>xn,因此,an+1=an+xn-1<an+
=an(1+
),
结合a1=b2-1及{bn}是公比1+
的等比数列可得,a2<a1(1+
)<b2(1+
)=b3,a3<a2(1+
)<b3(1+
)=b4,…,
从而对任意的m=1,2,…,n-1,都有am<bm+1…(11分)
另一方面,因为bn<an?xn(1+
) n-1<xn+xn-1-1+(m-1)xn-1
?xn-m+1(1+x)m-1<xn+mxn-1-1m=1,2,…n,其中n为给定的不小于
3的正整数)?x(1+x)n-1<xn+nxn-1-1
?xn+(n-1)xn-1+
xn-2+…+x<xn+nxn-1-1?
xn-2+x+1<xn-1(*)
显然,(*)式左边是关于x的n-2次式,右边是关于x的n-1次式,
只要正整数x充分大,(*) 式即可成立,从而m=1,2,…,n时,都有bn<an.
综上,必存在正整数x,满足b1<a1<b 2<a2<…bn<an. …(16分)
| 1 |
| x |
依题意有1<a1<b2<a1+1<b22<a1+2<b23<a1+3<b24<…(2分)
从而1<b2<2<b22<3<b23<4<…
即1<b2<2①,
| 2 |
| 3 |
| 3 | 3 |
| 3 | 4 |
| 2 |
| 4 | 5 |
| 5 | 5 |
| 5 | 6 |
由①②③④得,
| 3 | 3 |
| 4 | 5 |
| 5 | 6 |
| 3 | 3 |
(2)依题意,am=xn+xn-1-1+(m-1)•xn-1,bm=xn(1+
| 1 |
| x |
一方面,当x∈N*时,an>xn,因此,an+1=an+xn-1<an+
| an |
| x |
| 1 |
| x |
结合a1=b2-1及{bn}是公比1+
| 1 |
| x |
| 1 |
| x |
| 1 |
| x |
| 1 |
| x |
| 1 |
| x |
从而对任意的m=1,2,…,n-1,都有am<bm+1…(11分)
另一方面,因为bn<an?xn(1+
| 1 |
| x |
?xn-m+1(1+x)m-1<xn+mxn-1-1m=1,2,…n,其中n为给定的不小于
3的正整数)?x(1+x)n-1<xn+nxn-1-1
?xn+(n-1)xn-1+
| n(n-1) |
| 2 |
| n(n-1) |
| 2 |
显然,(*)式左边是关于x的n-2次式,右边是关于x的n-1次式,
只要正整数x充分大,(*) 式即可成立,从而m=1,2,…,n时,都有bn<an.
综上,必存在正整数x,满足b1<a1<b 2<a2<…bn<an. …(16分)
点评:本题主要考查了等差数列与等比数列的想通项公式及性质的综合应用,解题的关键是具备较强的逻辑推理的能力

练习册系列答案
相关题目
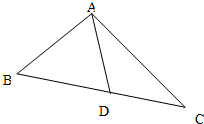 如图,在△ABC中,已知∠B=45°,D是BC边上的一点,AD=10,AC=14,DC=6.
如图,在△ABC中,已知∠B=45°,D是BC边上的一点,AD=10,AC=14,DC=6.