题目内容
三个工程队要承包5项不同的工程,每队至少承包一项,问共有多少种不同的承包方案.
考点:排列、组合及简单计数问题
专题:应用题,排列组合
分析:第一步要将五项工程分为三组,第二步再计算承包的方法,由于五项工程分为三组的分法可能是3,1,1或2,2,1故要分为两类计数.
解答:
解:若五项工程分为三组,每组的工程数分别为3,1,1,则不同的分法有C53=10种,故不同的承包方案有10A33=60种;
若五项工程分为三组,每组的工程数分别为2,2,1,则不同的分法有
C52C32=15种,故不同的承包方案15A33=90种.
故总的不同承包方案为60+90=150种.
若五项工程分为三组,每组的工程数分别为2,2,1,则不同的分法有
| 1 |
| 2 |
故总的不同承包方案为60+90=150种.
点评:本题考查排列组合及简单计数问题,解题的关键是将问题分为两类计数,在第二类2,2,1分组中由于计数重复了一倍,故应除以2,此是本题中的易错点,疑点,解题时要注意避免重复,这是计数问题中常犯的错误.

练习册系列答案
相关题目
给出下列命题:
①函数y=2-|x|为偶函数;
②函数y=1是周期函数;
③函数f(x)=2x-x2的零点有2个;
④函数g(x)=|log2x|-(
)x在(0,+∞)上恰有两个零点x1,x2且x1•x2<1.
其中正确命题的个数是( )
①函数y=2-|x|为偶函数;
②函数y=1是周期函数;
③函数f(x)=2x-x2的零点有2个;
④函数g(x)=|log2x|-(
| 1 |
| 2 |
其中正确命题的个数是( )
| A、1 | B、2 | C、3 | D、4 |
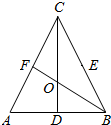 在△ABC中,D、E、F分别是AB、BC、CA的中点,BF与CD交于点O,设向量
在△ABC中,D、E、F分别是AB、BC、CA的中点,BF与CD交于点O,设向量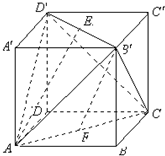 正方体ABCD-A′B′C′D′的棱长等于2,E,F分别是B′D′,AC的中点.求:
正方体ABCD-A′B′C′D′的棱长等于2,E,F分别是B′D′,AC的中点.求: