题目内容
一只不透明的口袋中装有形状、大小、质地都相同的8只小球,其中3只白球,3只红球和2只黄球,现从中一次随机摸出2只球.求:
(1)2只球都是红球的概率;
(2)2只球不同颜色的概率.
(1)2只球都是红球的概率;
(2)2只球不同颜色的概率.
考点:古典概型及其概率计算公式
专题:函数的性质及应用
分析:(1)用组合的方法求出摸出两个球的基本事件和两球都是红色的基本事件,由古典概型的概率公式求出概率.
(2)用组合的方法求出摸出两个球的基本事件和两球颜色不同的基本事件,由古典概型的概率公式求出概率.
(2)用组合的方法求出摸出两个球的基本事件和两球颜色不同的基本事件,由古典概型的概率公式求出概率.
解答:
解:从形状大小都相同的8只小球中一次随机摸出2只球,共
=28种
(1)从形状大小都相同的8只小球中一次随机摸出2只球,则2只球都是红色共有
=3种
故2只球均为红色的概率为P=
;
(2)“2只球颜色相同”共有
+
+
=7种
故2只球不同颜色的事件有28-7=21种,
故2只球不同颜色的概率P=
=
.
| C | 2 8 |
(1)从形状大小都相同的8只小球中一次随机摸出2只球,则2只球都是红色共有
| C | 2 3 |
故2只球均为红色的概率为P=
| 3 |
| 28 |
(2)“2只球颜色相同”共有
| C | 2 3 |
| C | 2 3 |
| C | 2 2 |
故2只球不同颜色的事件有28-7=21种,
故2只球不同颜色的概率P=
| 21 |
| 28 |
| 3 |
| 4 |
点评:求一个事件的概率时,应该先判断出事件的概率模型,然后选择合适的概率公式进行计算.

练习册系列答案
 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案
相关题目
时钟的时针和分针一天24小时内重合( )次.
| A、21 | B、22 | C、23 | D、24 |
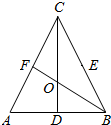 在△ABC中,D、E、F分别是AB、BC、CA的中点,BF与CD交于点O,设向量
在△ABC中,D、E、F分别是AB、BC、CA的中点,BF与CD交于点O,设向量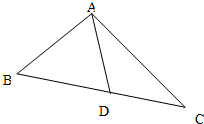 如图,在△ABC中,已知∠B=45°,D是BC边上的一点,AD=10,AC=14,DC=6.
如图,在△ABC中,已知∠B=45°,D是BC边上的一点,AD=10,AC=14,DC=6.