题目内容
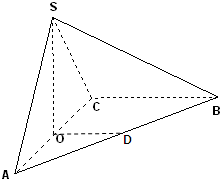 在三棱锥S-ABC中,平面SAC⊥平面ABC,且△SAC是正三角形,O是AC的中点,D是AB的中点.
在三棱锥S-ABC中,平面SAC⊥平面ABC,且△SAC是正三角形,O是AC的中点,D是AB的中点.(Ⅰ) 求证:OD∥平面SBC;
(Ⅱ) 求证:SO⊥AB.
考点:直线与平面平行的判定
专题:空间位置关系与距离
分析:(I)由题设条件推导出OD是△ABC的中位线,进而利用线面平行的判定定理得到OD∥平面SBC;
(Ⅱ)由等边三角形三线合一,可得SO⊥AC,结合面面垂直的性质定理可得SO⊥平面ABC,再由线面垂直的性质可得SO⊥AB.
(Ⅱ)由等边三角形三线合一,可得SO⊥AC,结合面面垂直的性质定理可得SO⊥平面ABC,再由线面垂直的性质可得SO⊥AB.
解答:
证明:(I)∵O是AC的中点,D是AB的中点.
∴OD∥BC,
又∵OD?平面SBC,BC?平面SBC,
∴OD∥平面SBC;
(Ⅱ)∵△SAC是正三角形,O是AC的中点,
∴SO⊥AC,
又∵平面SAC⊥平面ABC,平面SAC∩平面ABC=AC,SO?平面SAC,
∴SO⊥平面ABC,
又∵AB?平面ABC,
∴SO⊥AB
∴OD∥BC,
又∵OD?平面SBC,BC?平面SBC,
∴OD∥平面SBC;
(Ⅱ)∵△SAC是正三角形,O是AC的中点,
∴SO⊥AC,
又∵平面SAC⊥平面ABC,平面SAC∩平面ABC=AC,SO?平面SAC,
∴SO⊥平面ABC,
又∵AB?平面ABC,
∴SO⊥AB
点评:本题考查直线与平面平行的证明,线面垂直的判定与性质,面面垂直的性质定理,解题时要认真审题,仔细解答,注意对空间线面关系判定及性质的合理运用.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
复数z=-1+i(i为虚数单位)在复平面上对应的点落在( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
∫
sin2xdx等于( )
π -π |
| A、0 | B、2π | C、4π | D、4 |