题目内容
为了让更多的人参与2010年在上海举办的“世博会”,上海某旅游公司面向国内外发行总量为2000万张的旅游优惠卡,其中向境外人士发行的是世博金卡(简称金卡),向境内人士发行的是世博银卡(简称银卡).现有一个由36名游客组成的旅游团到上海参观旅游,其中
是境外游客,其余是境内游客.在境外游客中有
持金卡,在境内游客中有
持银卡.
(1)在该团的境内游客中随机采访3名游客,求其中持银卡人数恰为2人的概率;
(2)在该团中随机采访3名游客,求恰有1人持金卡且持银卡者少于2人的概率.
| 3 |
| 4 |
| 1 |
| 3 |
| 2 |
| 3 |
(1)在该团的境内游客中随机采访3名游客,求其中持银卡人数恰为2人的概率;
(2)在该团中随机采访3名游客,求恰有1人持金卡且持银卡者少于2人的概率.
考点:相互独立事件的概率乘法公式
专题:概率与统计
分析:由题意得,境外游客有27人,其中9人持金卡;境内游客有9人,其中6人持银卡,求出在该团的境内游客中随机采访3名游客的基本事件总数,
(1)求出持银卡人数恰为2人的基本事件个数,代入古典概型概率计算公式,可得答案.
(2)求出恰有1人持金卡且持银卡者少于2人的基本事件个数,代入古典概型概率计算公式,可得答案.
(1)求出持银卡人数恰为2人的基本事件个数,代入古典概型概率计算公式,可得答案.
(2)求出恰有1人持金卡且持银卡者少于2人的基本事件个数,代入古典概型概率计算公式,可得答案.
解答:
解:由题意得,省外游客有27人,其中9人持金卡;省内游客有9人,其中6人持银卡.
在该团的境内游客中随机采访3名游客的基本事件共有
=7140种,
(1)其中持银卡人数恰为2人的基本事件个数为:
=450种,
故其中持银卡人数恰为2人的概率P=
=
,
(2)其中恰有1人持金卡且持银卡者少于2人的基本事件个数为:
+
=3024,
故恰有1人持金卡且持银卡者少于2人的概率P=
=
.
在该团的境内游客中随机采访3名游客的基本事件共有
| C | 3 36 |
(1)其中持银卡人数恰为2人的基本事件个数为:
| C | 2 6 |
| C | 1 30 |
故其中持银卡人数恰为2人的概率P=
| 450 |
| 7140 |
| 15 |
| 238 |
(2)其中恰有1人持金卡且持银卡者少于2人的基本事件个数为:
| C | 1 9 |
| C | 2 21 |
| C | 1 9 |
| C | 1 21 |
| C | 1 6 |
故恰有1人持金卡且持银卡者少于2人的概率P=
| 3024 |
| 7140 |
| 36 |
| 85 |
点评:本题考查的知识点是古典概型概率计算公式,其中熟练掌握利用古典概型概率计算公式求概率的步骤,是解答的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
椭圆C的两个焦点分别是F1,F2,若C上的点P满足|PF1|=
|F1F2|,则椭圆C的离心率e的取值范围是( )
| 3 |
| 2 |
A、e≤
| ||||
B、e≥
| ||||
C、
| ||||
D、0<e≤
|
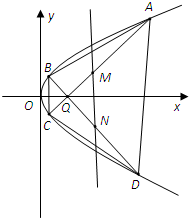 已知抛物线y2=2px(p>0)上的任意一点P到该抛物线焦点的距离比该点到y轴的距离多1.
已知抛物线y2=2px(p>0)上的任意一点P到该抛物线焦点的距离比该点到y轴的距离多1.