题目内容
数列{an}中,已知a1=2,当n≥2时,an=
an-1+
.数列{bn}满足bn=3n-1an(n∈N*)
(Ⅰ)证明:{bn}为等差数列,并求{bn}的通项公式;
(Ⅱ)记数列{
}的前n项和为Sn,是否存在正整数m,n使得
<
成立?若存在,求出所有符合条件的有序实数对(m,n);若不存在,请说明理由.
| 1 |
| 3 |
| 2 |
| 3n-1 |
(Ⅰ)证明:{bn}为等差数列,并求{bn}的通项公式;
(Ⅱ)记数列{
| an |
| n |
| Sn-m |
| Sn+1-m |
| 3m |
| 3m+1 |
考点:数列的求和,数列递推式,数列与不等式的综合
专题:点列、递归数列与数学归纳法
分析:(Ⅰ)根据递推数列,结合等差数列的定义即可证明{bn}为等差数列,即可求{bn}的通项公式;
(Ⅱ)求出数列{
}的通项公式,以及前n项和为Sn,将不等式恒成立问题进行转化,即可得到结论.
(Ⅱ)求出数列{
| an |
| n |
解答:
解:(Ⅰ)当n=1时,b1=30a1=2,
当n≥2时,在an=
an-1+
的两边同乘以3n-1得,3n-1an=
×3n-1an-1+
×3n-1,
得3n-1an=3n-2an-1+2,
即bn-bn-1=2,(n≥2),
即{bn}为等差数列,首项为2,公差为2,
则{bn}的通项公式为bn=2+2(n-1)=2n.
(Ⅱ)由(Ⅰ)得bn=3n-1an=2n,故
=
,
∴数列{
}的前n项和为Sn=
=3(1-
),
则
=
=1-
=1-
,
∵
<
=1-
,得
>
,
∴(3-m)•3m-1>0,
∵m是正整数,∴m=1,2,
当m=1时,
>
,解得n=1,
当m=2时,
>
,解得n=1,2.
综上存在所有符合条件的有序实数对(m,n)为:(1,1),(2,1),(2,2).
当n≥2时,在an=
| 1 |
| 3 |
| 2 |
| 3n-1 |
| 1 |
| 3 |
| 2 |
| 3n-1 |
得3n-1an=3n-2an-1+2,
即bn-bn-1=2,(n≥2),
即{bn}为等差数列,首项为2,公差为2,
则{bn}的通项公式为bn=2+2(n-1)=2n.
(Ⅱ)由(Ⅰ)得bn=3n-1an=2n,故
| an |
| n |
| 2 |
| 3n-1 |
∴数列{
| an |
| n |
2(1-
| ||
1-
|
| 1 |
| 3n |
则
| Sn-m |
| Sn+1-m |
3-m-
| ||
3-m-
|
| ||||
3-m-
|
| 2 |
| (3-m)3n-1 |
∵
| Sn-m |
| Sn+1-m |
| 3m |
| 3m+1 |
| 1 |
| 3m+1 |
| 2 |
| (3-m)•3n-1 |
| 1 |
| 3m+1 |
∴(3-m)•3m-1>0,
∵m是正整数,∴m=1,2,
当m=1时,
| 1 |
| 2•3n-1 |
| 1 |
| 4 |
当m=2时,
| 2 |
| 3n-1 |
| 1 |
| 10 |
综上存在所有符合条件的有序实数对(m,n)为:(1,1),(2,1),(2,2).
点评:本题主要考查等差数列的判断和通项公式的求解,以及不等式恒成立的证明,考查学生的综合应用.

练习册系列答案
相关题目
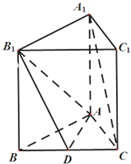 如图所示,在直三棱柱(侧棱与底面垂直的三棱柱)ABC-A1B1C1中,AB=8,AC=6,BC=10,D是BC边的中点.
如图所示,在直三棱柱(侧棱与底面垂直的三棱柱)ABC-A1B1C1中,AB=8,AC=6,BC=10,D是BC边的中点.