题目内容
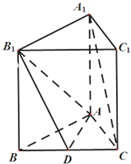 如图所示,在直三棱柱(侧棱与底面垂直的三棱柱)ABC-A1B1C1中,AB=8,AC=6,BC=10,D是BC边的中点.
如图所示,在直三棱柱(侧棱与底面垂直的三棱柱)ABC-A1B1C1中,AB=8,AC=6,BC=10,D是BC边的中点.(1)求证:AB⊥
| A | 1 |
(2)求证:A1C∥平面AB1D.
考点:直线与平面平行的判定
专题:空间位置关系与距离
分析:(1)先证明出AB⊥AC和AA1⊥AB利用先线面垂直的判定定理证明出AB⊥平面A1ACC1最后根据线面垂直的性质证明出AB⊥A1C.
(2)连结A1B交AB1于点E,再连结DE,先利用中位线的性质证明出ED∥A1C,继而可利用线面平行的判定定理证明出A1C∥平面AB1D.
(2)连结A1B交AB1于点E,再连结DE,先利用中位线的性质证明出ED∥A1C,继而可利用线面平行的判定定理证明出A1C∥平面AB1D.
解答:
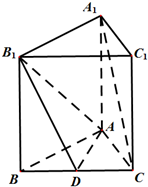 证明:(1)∵AB=8,AC=6,BC=10,
证明:(1)∵AB=8,AC=6,BC=10,
∴AB2+AC2=BC2
∴AB⊥AC,
∵在直三棱柱ABC-A1B1C1中,AA1⊥面ABCAB?面ABC,
∴AA1⊥AB
又∵AA1∩AC=AAA1?面A1ACC1AC?面A1ACC1
∴AB⊥平面A1ACC1
且A1C?面A1ACC1
∴AB⊥A1C.
(2)连结A1B交AB1于点E,再连结DE,
∵D是BC边的中点.
∴DE为△BCA1的中位线,
∴ED∥A1C,
∵ED?平面AB1D,且A1C?平面AB1D,
∴A1C∥面AB1D.
 证明:(1)∵AB=8,AC=6,BC=10,
证明:(1)∵AB=8,AC=6,BC=10,∴AB2+AC2=BC2
∴AB⊥AC,
∵在直三棱柱ABC-A1B1C1中,AA1⊥面ABCAB?面ABC,
∴AA1⊥AB
又∵AA1∩AC=AAA1?面A1ACC1AC?面A1ACC1
∴AB⊥平面A1ACC1
且A1C?面A1ACC1
∴AB⊥A1C.
(2)连结A1B交AB1于点E,再连结DE,
∵D是BC边的中点.
∴DE为△BCA1的中位线,
∴ED∥A1C,
∵ED?平面AB1D,且A1C?平面AB1D,
∴A1C∥面AB1D.
点评:本题主要考查了线面平行和线面垂直的判定定理的运用,考查了学生空间观察能力和分析的能力.

练习册系列答案
相关题目
某地气象台预报“本市明天有雨的概率是95%”.以下理解正确的是( )
| A、本市明天将有95%的地区有雨 |
| B、本市明天将有95%的时间有雨 |
| C、明天出行不带雨具肯定会淋雨 |
| D、明天出行不带雨具淋雨的可能性较大 |
已知F1,F2是双曲线
-
=1(a>0,b>0)的两个焦点,PQ是经过F1且垂直于x轴的双曲线的弦,如果∠PF2Q=90°,则双曲线的离心率( )
| x2 |
| a2 |
| y2 |
| b2 |
A、2
| ||
B、1+
| ||
C、1+
| ||
D、2+2
|
已知f(x)为偶函数,f(2)+f(-5)=4,求f(-2)+f(5)=( )
| A、4 | B、-4 | C、2 | D、-5 |
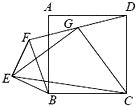 如图,四边形ABCD是正方形,△BEF是等腰直角三角形,∠BEF=90°,BE=EF.连接DF,G为DF的重点,连接EG,CG,EC,求证:|
如图,四边形ABCD是正方形,△BEF是等腰直角三角形,∠BEF=90°,BE=EF.连接DF,G为DF的重点,连接EG,CG,EC,求证:|