题目内容
4.已知各项都不相等的数列{an}满足n≥2,$a_n^2+a_{n-1}^2-2{a_n}{a_{n-1}}-{a_n}+{a_{n-1}}=0$,a1=3.(1)求数列的通项公式an;
(2)若${b_n}=\frac{1}{{n{a_n}}}$,求数列{bn}的前n项和Sn;
(3)证明:${S_n}≥\frac{1}{3}$.
分析 (Ⅰ)由$a_n^2+a_{n-1}^2-2{a_n}{a_{n-1}}-{a_n}+{a_{n-1}}=0$,得${({a_n}-{a_{n-1}})^2}-({a_n}-{a_{n-1}})=0$,(an-an-1)(an-an-1-1)=0,即an-an-1=1,
(Ⅱ)${b_n}=\frac{1}{{n{a_n}}}=\frac{1}{n(n+2)}=\frac{1}{2}({\frac{1}{n}-\frac{1}{n+2}})$.累加即可求和Sn
(Ⅲ)证明:由(Ⅱ)知,${S_n}=\frac{1}{2}({1+\frac{1}{2}-\frac{1}{n+1}-\frac{1}{n+2}})=\frac{3}{4}-\frac{1}{2}({\frac{1}{n+1}+\frac{1}{n+2}})$单调递增,求出Sn最小值即可
解答 解:(Ⅰ)由$a_n^2+a_{n-1}^2-2{a_n}{a_{n-1}}-{a_n}+{a_{n-1}}=0$,
得${({a_n}-{a_{n-1}})^2}-({a_n}-{a_{n-1}})=0$,(an-an-1)(an-an-1-1)=0,
解得an-an-1=0(舍)或an-an-1-1=0,即an-an-1=1,
因此数列{an}是公差为1的等差数列,an=n+2.
(Ⅱ)${b_n}=\frac{1}{{n{a_n}}}=\frac{1}{n(n+2)}=\frac{1}{2}({\frac{1}{n}-\frac{1}{n+2}})$.
∴Sn=b1+b2+…+bn=$\frac{1}{2}[{({1-\frac{1}{3}})+({\frac{1}{2}-\frac{1}{4}})+({\frac{1}{3}-\frac{1}{5}})+…+({\frac{1}{n}-\frac{1}{n+2}})}]$
=$\frac{1}{2}({1+\frac{1}{2}-\frac{1}{n+1}-\frac{1}{n+2}})$
=$\frac{3}{4}-\frac{2n+3}{2(n+1)(n+2)}$
(Ⅲ)证明:由(Ⅱ)知,${S_n}=\frac{1}{2}({1+\frac{1}{2}-\frac{1}{n+1}-\frac{1}{n+2}})=\frac{3}{4}-\frac{1}{2}({\frac{1}{n+1}+\frac{1}{n+2}})$单调递增,
${({S_n})_{min}}={S_1}=\frac{3}{4}-\frac{1}{2}({\frac{1}{2}+\frac{1}{3}})=\frac{1}{3}$,
所以${S_n}≥\frac{1}{3}$.
点评 本题考查了数列的递推式、裂项求和、证明数列不等式,属于中档题.

| A. | $\frac{2π}{3}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{3}$ |
| A. | $\frac{4}{3}$ | B. | $-\frac{4}{3}$ | C. | $\frac{3}{4}$ | D. | $-\frac{3}{4}$ |
| A. | sinθ-cosθ | B. | cosθ-sinθ | C. | ±(sinθ-cosθ) | D. | sinθ+cosθ |
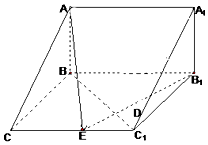 如图,在三棱柱ABC-A1B1C1中,已知AB⊥侧面BB1C1C,CB⊥C1B,BC=1,CC1=2,A1B1=$\sqrt{2}$,
如图,在三棱柱ABC-A1B1C1中,已知AB⊥侧面BB1C1C,CB⊥C1B,BC=1,CC1=2,A1B1=$\sqrt{2}$,