题目内容

13．已知$θ∈[{\frac{π}{2}，π}]$，则$\sqrt{1+2sin（{π+θ}）sin（{\frac{π}{2}-θ}）}$=（　　）
A．sinθ-cosθB．cosθ-sinθC．±（sinθ-cosθ）D．sinθ+cosθ

分析 直接由三角函数的诱导公式化简结合已知条件计算即可得答案．

解答 解：由$θ∈[{\frac{π}{2}，π}]$，$\sqrt{1+2sin（{π+θ}）sin（{\frac{π}{2}-θ}）}$=$\sqrt{1+2（-sinθ）cosθ}$=$\sqrt{（sinθ-cosθ）^{2}}$=|sinθ-cosθ|=sinθ-cosθ，
故选：A．

点评 本题考查了三角函数的化简求值，考查了三角函数的诱导公式的运用，是基础题．

练习册系列答案
相关题目
3．已知集合A={-1，0，1}，B={y|y=|x|}，则A∩B=（　　）
A．{0}B．{1}C．{0，1}D．{-1，0，1}
4．已知各项都不相等的数列{an}满足n≥2，$a_n^2+a_{n-1}^2-2{a_n}{a_{n-1}}-{a_n}+{a_{n-1}}=0$，a1=3．
（1）求数列的通项公式an；
（2）若${b_n}=\frac{1}{{n{a_n}}}$，求数列{bn}的前n项和Sn；
（3）证明：${S_n}≥\frac{1}{3}$．
1．已知φ∈（0，π），且$tan（φ+\frac{π}{4}）=-\frac{1}{3}$．
（Ⅰ）求tan2φ的值；
（Ⅱ）求$\frac{sinφ+cosφ}{2cosφ-sinφ}$的值．
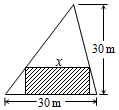8．在如图所示的三角形空地中，欲建一个面积不小于200m2的内接矩形花园（阴影部分），则其边长x（单位：m）的取值范围是[10，20]．
18．已知函数f（x）=2tan（ωx+ϕ）$（{ω＞0，|ϕ|＜\frac{π}{2}}）$的最小正周期为$\frac{π}{2}$，且$f（{\frac{π}{2}}）=-2$，则ω=2，ϕ=-$\frac{π}{4}$．
5．已知二次函数f（x）=x2-2x+3
（Ⅰ）若函数$y=f（{log_3}x+m），x∈[\frac{1}{3}，3]$的最小值为3，求实数m的值；
（Ⅱ）若对任意互不相同的x1，x2∈（2，4），都有|f（x1）-f（x2）|＜k|x1-x2|成立，求实数k的取值范围．
2．已知圆心C的坐标为（2，-2），圆C与x轴和y轴都相切
（1）求圆C的方程
（2）求与圆C相切，且在x轴和y轴上的截距相等的直线方程．
19．圆的半径为6cm，则圆心角为30°的扇形面积为3π．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网