题目内容
14.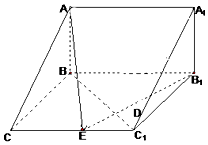 如图,在三棱柱ABC-A1B1C1中,已知AB⊥侧面BB1C1C,CB⊥C1B,BC=1,CC1=2,A1B1=$\sqrt{2}$,
如图,在三棱柱ABC-A1B1C1中,已知AB⊥侧面BB1C1C,CB⊥C1B,BC=1,CC1=2,A1B1=$\sqrt{2}$,(1)试在棱CC1(不包含端点C,C1)上确定一点E的位置,使得EA⊥EB1;
(2)在(Ⅰ)的条件下,求AE和BC1所成角.
分析 (1)由EA⊥EB1,AB⊥EB1,AB∩AE=A,AB,AE?平面ABE,从而B1E⊥平面ABE且BE?平面ABE,故BE⊥B1E.利用余弦定理及其勾股定理即可得出.
(2)取BC中点D,则DE∥BC1,连接AD,所以∠AED或其补角为异面直线AE和BC1所成角所成的角.
利用余弦定理即可得出.
解答 解:(1)由EA⊥EB1,AB⊥EB1,AB∩AE=A,AB,AE?平面ABE,
从而B1E⊥平面ABE且BE?平面ABE,故BE⊥B1E .
.
不妨设 CE=x,则C1E=2-x,
∵∠BCC1=60°,∴BE2=1+x2-x,
∵∠BCC1=60°,∴∠B1C1C=120°,∴${B_1}{E^2}={x^2}-5x+7$.
在Rt△BEB1中有1+x2-x+x2-5x+7=4,
从而x=1或x=2(当x=2时E与C1重合不满足题意).
故E为CC1的中点时,EA⊥EB1.
(2)取BC中点D,则DE∥BC1,连接AD,
所以∠AED或其补角为异面直线AE和BC1所成角所成的角.
∵$AE=\sqrt{3},DE=\frac{{\sqrt{3}}}{2},AD=\frac{3}{2}$,
∴cos∠AED=$\frac{(\frac{\sqrt{3}}{2})^{2}+(\sqrt{3})^{2}-(\frac{3}{2})^{2}}{2×\frac{\sqrt{3}}{2}×\sqrt{3}}$=$\frac{1}{2}$,
∴∠AED=60°.
点评 本题考查了空间位置关系、空间角、余弦定理与勾股定理,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
4.已知奇函数f(x)在(0,+∞)上是增函数,且f(2)=0,则f(x)>0的解集为( )
| A. | (0,2) | B. | (-2,0) | C. | (-2,0)∪(2,+∞) | D. | (-2,2) |
2.一条直线与两条异面直线中的一条平行,则它和另一条的位置关系是( )
| A. | 异面 | B. | 相交 | C. | 异面或平行 | D. | 相交或异面 |
19.一个几何体的三视图如图,则该几何体的体积为( )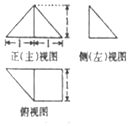

| A. | 2 | B. | $\frac{3}{2}$ | C. | 1 | D. | $\frac{1}{2}$ |
3.已知集合A={-1,0,1},B={y|y=|x|},则A∩B=( )
| A. | {0} | B. | {1} | C. | {0,1} | D. | {-1,0,1} |
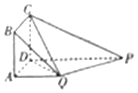 如图,四边形ABCD为正方形,QA⊥平面ABCD,PD∥QA,2QA=2AB=PD
如图,四边形ABCD为正方形,QA⊥平面ABCD,PD∥QA,2QA=2AB=PD