题目内容
二直线mx+3y+3=0，2x+（m-1）y+2=0平行，则实数m的值为（ ）
| A、3或-2 | B、-3或2 |
| C、3 | D、-2 |
考点：直线的一般式方程与直线的平行关系
专题：直线与圆
分析：根据两直线平行，且直mx+3y+3=0的斜率存在，故它们的斜率相等，解方程求得m的值．
解答：
解：直线mx+3y+3=0的斜率是-
，直线2x+（m-1）y+2=0的斜率是
∵二直线mx+3y+3=0，2x+（m-1）y+2=0平行
∴-
=
解得：m=-2或3，
当m=3时两直线重合，故舍去，所以m=-2，
故选：D．
| m |
| 3 |
| 2 |
| 1-m |
∵二直线mx+3y+3=0，2x+（m-1）y+2=0平行
∴-
| m |
| 3 |
| 2 |
| 1-m |
解得：m=-2或3，
当m=3时两直线重合，故舍去，所以m=-2，
故选：D．
点评：本题的考点是直线的一般式方程与直线的平行关系，主要考查两直线平行的性质，两直线平行，它们的斜率相等或者都不存在．
练习册系列答案
阅读快车系列答案
相关题目
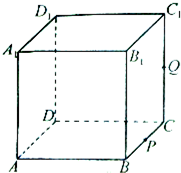如图，正方体ABCD-A1B1C1D1的棱长为1，P为BC的中点，Q为线段CC1上的动点，过点A，P，Q的平面截该正方体所得的截面记为S．则下列命题正确的是
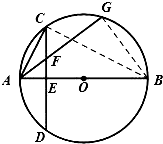已知，AB为圆O的直径，CD为垂直AB的一条弦，垂足为E，弦AG交CD于F．
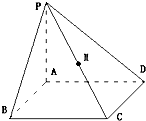如图，四棱锥P-ABCD中，四边形ABCD是矩形，PA⊥平面ABCD，且AP=
