题目内容
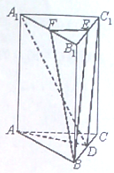 如图,在三棱柱ABC-A1B1C1中,底面为正三角形,AA1⊥平面ABC,D,E,F分别为BC,B1C1,A1B1的中点.
如图,在三棱柱ABC-A1B1C1中,底面为正三角形,AA1⊥平面ABC,D,E,F分别为BC,B1C1,A1B1的中点.(1)求证:BC⊥A1D;
(2)求证:平面BEF∥平面DA1C1.
考点:平面与平面平行的判定,空间中直线与直线之间的位置关系
专题:空间位置关系与距离
分析:(1)充分利用已知三棱柱ABC-A1B1C1中,底面为正三角形,AA1⊥平面ABC,D,E,F分别为BC,B1C1,A1B1的中点.只要证明BC⊥平面DAA1 即可;
(2)利用面面平行的判断,只要证明EF∥平面DA1C1 和BE∥平面DA1C1即可.
(2)利用面面平行的判断,只要证明EF∥平面DA1C1 和BE∥平面DA1C1即可.
解答:
证明:(1)∵△ABC为正三角形,D是BC的中点
∴BC⊥AD,…(1分)
∵AA1⊥平面ABC,BC?平面ABC,
∴BC⊥AA1 …(3分)
∵AD,AA1是平面DAA1内的两条相交直线,
∴BC⊥平面DAA1 …(5分)
∵A1D?平面DAA1
∴BC⊥A1D …(6分)
(2)∵D,E,F分别为BC,B1C1,A1B1的中点,
∴EF是△A1B1C1的边A1C1的中位线
∴EF∥A1C1 …(7分)
∵A1C1?平面DA1C1,EF?平面DA1C1,
∴EF∥平面DA1C1,…(8分)
∵EC1∥BD且EC1=BD
∴四边形BDC1E为平行四边形
∴BE∥DC1 …(9分)
∵DC1?平面DA1C1,BE?平面DA1C1,
∴BE∥平面DA1C1,…(10分)
∵BE,EF是平面BEF的两条相交直线
∴平面BEF∥平面DA1C1 …(12分)
∴BC⊥AD,…(1分)
∵AA1⊥平面ABC,BC?平面ABC,
∴BC⊥AA1 …(3分)
∵AD,AA1是平面DAA1内的两条相交直线,
∴BC⊥平面DAA1 …(5分)
∵A1D?平面DAA1
∴BC⊥A1D …(6分)
(2)∵D,E,F分别为BC,B1C1,A1B1的中点,
∴EF是△A1B1C1的边A1C1的中位线
∴EF∥A1C1 …(7分)
∵A1C1?平面DA1C1,EF?平面DA1C1,
∴EF∥平面DA1C1,…(8分)
∵EC1∥BD且EC1=BD
∴四边形BDC1E为平行四边形
∴BE∥DC1 …(9分)
∵DC1?平面DA1C1,BE?平面DA1C1,
∴BE∥平面DA1C1,…(10分)
∵BE,EF是平面BEF的两条相交直线
∴平面BEF∥平面DA1C1 …(12分)
点评:本题考查了三棱柱中的线线垂直和面面平行的判断,关键是熟练运用三棱柱的性质以及线面垂直和线面平行的判定定理解答.

练习册系列答案
相关题目
球的半径为2,它的内接圆柱的底面半径为1,则圆柱的侧面积为( )
A、2
| ||
B、4
| ||
| C、12π | ||
| D、24π |

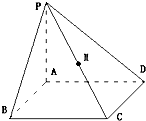 如图,四棱锥P-ABCD中,四边形ABCD是矩形,PA⊥平面ABCD,且AP=
如图,四棱锥P-ABCD中,四边形ABCD是矩形,PA⊥平面ABCD,且AP=