题目内容
设集合A={1，3，a}，B={1，2}且A?B，则a的值为（ ）
| A、0 | B、1 | C、2 | D、3 |
考点：集合的包含关系判断及应用
专题：函数的性质及应用
分析：本题由集合间的关系可以得到元素与集合的关系，从而求出实数a的值，得到本题结论．
解答：
解：∵B={1，2}，
∴2∈B，
∵A?B，
∴2∈A．
∵集合A={1，3，a}，
∴a=2．
故选C．
∴2∈B，
∵A?B，
∴2∈A．
∵集合A={1，3，a}，
∴a=2．
故选C．
点评：本题考查了集合与集合的关系、集合与元素的关系，本题难度不大，属于基础题．
练习册系列答案
相关题目
已知函数f（x）在R上满足f（x）=2f（-x）-x2则曲线y=f（x）在点（1，f（1））处的切线方程是（ ）
| A、y=x |
| B、y=2x-1 |
| C、y=3x-2 |
| D、y=-2x+3 |
命题p：?x∈R，x3+x-2≥0的否定是（ ）
| A、?x∈R，x3+x-2＜0 |
| B、?x∈R，x3+x-2≥0 |
| C、?x∈R，x3+x-2＜0 |
| D、?x∈R，x3+x-2≠0 |
函数y=3 x2-3x+2，x∈[-1，2]的值域是（ ）
| A、R | |||||
B、[
| |||||
| C、[9，243] | |||||
| D、[3，+∞） |
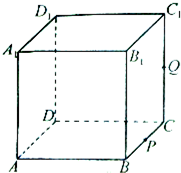如图，正方体ABCD-A1B1C1D1的棱长为1，P为BC的中点，Q为线段CC1上的动点，过点A，P，Q的平面截该正方体所得的截面记为S．则下列命题正确的是