题目内容
15. 为了参加某数学竞赛,某高级中学对高二年级理科、文科两个数学兴趣小组的同学进行了赛前模拟测试,成绩(单位:分)记录如下.
为了参加某数学竞赛,某高级中学对高二年级理科、文科两个数学兴趣小组的同学进行了赛前模拟测试,成绩(单位:分)记录如下.理科:79,81,81,79,94,92,85,89
文科:94,80,90,81,73,84,90,80
(1)画出理科、文科两组同学成绩的茎叶图;
(2)计算理科、文科两组同学成绩的平均数和方差,并从统计学的角度分析,哪组同学在此次模拟测试中发挥比较好;(参考公式:样本数据x1,x2,…,xn的方差:${s^2}=\frac{1}{n}[{({x_1}-\overline x)^2}+{({x_2}-\overline x)^2}+…+{({x_n}-\overline x)^2}]$,其中$\overline x$为样本平均数)
(3)若在成绩不低于90分的同学中随机抽出3人进行培训,求抽出的3人中既有理科组同学又有文科组同学的概率.
分析 (1)根据题意,画出理科、文科两组同学成绩的茎叶图即可;
(2)计算理科、文科同学成绩的平均数与方差,比较得出结论;
(3)得出成绩不低于90分的同学有理科2个,文科3个,用列举法求出基本事件数,求出对应的概率.
解答 解:(1)根据题意,画出理科、文科两组同学成绩的茎叶图,如图所示;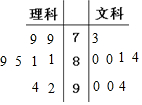
(2)计算理科同学成绩的平均数是$\overline{{x}_{1}}$=$\frac{1}{8}$×(79+79+81+81+85+89+92+94)=85,
方差是${{s}_{1}}^{2}$=$\frac{1}{8}$×[(79-85)2+(79-85)2+(81-85)2+(81-85)2+(85-85)2+(89-85)2+(92-85)2+(94-85)2]=31.25;
计算文科同学成绩的平均数是$\overline{{x}_{2}}$=$\frac{1}{8}$×(73+80+80+81+84+90+90+94)=84,
方差是${{s}_{2}}^{2}$=$\frac{1}{8}$×[(73-84)2+(80-84)2+(80-84)2+(81-84)2+(84-84)2+(90-84)2+(90-84)2+(94-84)2]=41.75;
所以从统计学的角度分析,理科同学在此次模拟测试中发挥比较好;
(3)成绩不低于90分的同学有理科2个,记为A、B,文科有3人,记为c、d、e;
从中随机抽出3人,基本事件为ABc、ABd、ABe、Acd、Ace、Ade、Bcd、Bce、Bde、cde共10种,
抽出的3人中既有理科组同学又有文科组同学是ABc、ABd、ABe、Acd、Ace、Ade、Bcd、Bce、Bde共9种,
故所求的概率为P=$\frac{9}{10}$.
点评 本题考查了茎叶图的应用问题,也考查了平均数与方差、概率的计算问题,是基础题.

| A. | $\frac{\sqrt{2}}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{4}$ | D. | $\frac{\sqrt{6}}{4}$ |
| A. | a2+3b≤0 | B. | a2+3b<0 | C. | a2+3b>0 | D. | a2+3b=0 |
| A. | 三角形的内角是第一象限角或第二象限角 | |
| B. | 第一象限的角是锐角 | |
| C. | 第二象限的角比第一象限的角大 | |
| D. | 角α是第四象限角的充要条件是$2kπ-\frac{π}{2}<α<2kπ(k∈z)$ |
| A. | 1-i | B. | 1+i | C. | -1+i | D. | -1-i |
| A. | -2 | B. | 4 | C. | 2 | D. | -4 |
| A. | -3<m<0 | B. | -3<m<2 | C. | -3<m<4 | D. | -1<m<3 |
| A. | ∅ | B. | [-2,0) | C. | [0,2] | D. | {0,1,2} |