题目内容
10.已知函数f(x)=ex-x2+ax,曲线y=f(x)在点(0,f(0))处的切线与x轴平行.(Ⅰ)求a的值;
(Ⅱ)若g(x)=ex-2x-1,求函数g(x)的最小值;
(Ⅲ)求证:存在c<0,当x>c时,f(x)>0.
分析 (Ⅰ)求得f(x)的导数,可得切线的斜率,由条件可得a的方程,解方程可得a的值;
(Ⅱ)求出g(x)的导数,可得单调区间和极值,且为最值;
(Ⅲ)显然g(x)=f'(x),且g(0)=0,运用零点存在定理可得g(x)的零点范围,可设g(x)=f'(x)存在两个零点,分别为0,x0.讨论x<0时,0<x<x0时,x>x0时,g(x)的符号,可得f(x)的极值,进而得到f(x)在(-∞,0)上单调递增,即可得证.
解答 解:(Ⅰ)函数f(x)=ex-x2+ax的导数为:
f′(x)=ex-2x+a,
由已知可得f′(0)=0,所以1+a=0,得a=-1.
(Ⅱ)g'(x)=ex-2,令g'(x)=0,得x=ln2,
所以x,g'(x),g(x)的变化情况如表所示:
| x | (-∞,ln2) | ln2 | (ln2,+∞) |
| g'(x) | - | 0 | + |
| g(x) | 递减 | 极小值 | 递增 |
(Ⅲ)证明:显然g(x)=f'(x),且g(0)=0,
由(Ⅱ)知,g(x)在(-∞,ln2)上单调递减,在(ln2,+∞)上单调递增.
又g(ln2)<0,g(2)=e2-5>0,
由零点存在性定理,存在唯一实数x0∈(ln2,2),满足g(x0)=0,
即${e^{x_0}}-2{x_0}-1=0$,${e^{x_0}}=2{x_0}+1$,
综上,g(x)=f'(x)存在两个零点,分别为0,x0.
所以x<0时,g(x)>0,即f'(x)>0,f(x)在(-∞,0)上单调递增;
0<x<x0时,g(x)<0,即f'(x)<0,f(x)在(0,x0)上单调递减;
x>x0时,g(x)>0,即f'(x)>0,f(x)在(x0,+∞)上单调递增,
所以f(0)是极大值,f(x0)是极小值,$f({x_0})={e^{x_0}}-{x_0}^2-{x_0}=2{x_0}+1-{x_0}^2-{x_0}=-{x_0}^2+{x_0}+1=-{({x_0}-\frac{1}{2})^2}+\frac{5}{4}$,
因为g(1)=e-3<0,$g(\frac{3}{2})={e^{\frac{3}{2}}}-4>0$,
所以${x_0}∈(1,\frac{3}{2})$,所以f(x0)>0,
因此x≥0时,f(x)>0.
因为f(0)=1且f(x)在(-∞,0)上单调递增,
所以一定存在c<0满足f(c)>0,
所以存在c<0,当x>c时,f(x)>0.
点评 本题考查导数的运用:求切线的斜率和单调区间、极值和最值,考查函数零点存在定理的运用,以及转化思想,考查化简整理的运算能力,属于难题.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案
相关题目
20.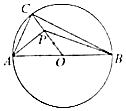 如图,AB为圆O的直径且AB=4,C为圆上不同于A、B的任意一点,若P为半径OC上的动点,则($\overrightarrow{PA}$+$\overrightarrow{PB}$)•$\overrightarrow{PC}$的最小值是( )
如图,AB为圆O的直径且AB=4,C为圆上不同于A、B的任意一点,若P为半径OC上的动点,则($\overrightarrow{PA}$+$\overrightarrow{PB}$)•$\overrightarrow{PC}$的最小值是( )
 如图,AB为圆O的直径且AB=4,C为圆上不同于A、B的任意一点,若P为半径OC上的动点,则($\overrightarrow{PA}$+$\overrightarrow{PB}$)•$\overrightarrow{PC}$的最小值是( )
如图,AB为圆O的直径且AB=4,C为圆上不同于A、B的任意一点,若P为半径OC上的动点,则($\overrightarrow{PA}$+$\overrightarrow{PB}$)•$\overrightarrow{PC}$的最小值是( )| A. | -4 | B. | -3 | C. | -2 | D. | -1 |
18.某三棱锥的三视图如图所示,则该三棱锥中最长棱的长度为( )
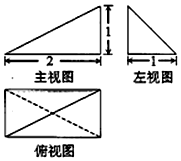

| A. | $\sqrt{5}$ | B. | $\sqrt{6}$ | C. | $2\sqrt{2}$ | D. | 3 |
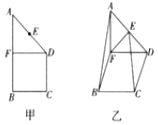 如图所示,在直角梯形ABCD中,AB∥CD,∠ABC=90°,CD=BC=1,点E为AD边上的中点,过点D作DF∥BC交AB于点F,现将此直角梯形沿DF折起,使得A-FD-B为直二面角,如图乙所示.
如图所示,在直角梯形ABCD中,AB∥CD,∠ABC=90°,CD=BC=1,点E为AD边上的中点,过点D作DF∥BC交AB于点F,现将此直角梯形沿DF折起,使得A-FD-B为直二面角,如图乙所示.