题目内容
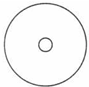 如图,半径为5cm的圆形纸板内有一个相同圆心的半径为1cm的小圆,现将半径为1cm的一枚硬币拋到此纸板上,使整块硬币随机完全落在纸板内,则硬币与小圆无公共点的概率为( )
如图,半径为5cm的圆形纸板内有一个相同圆心的半径为1cm的小圆,现将半径为1cm的一枚硬币拋到此纸板上,使整块硬币随机完全落在纸板内,则硬币与小圆无公共点的概率为( )A、
| ||
B、
| ||
C、
| ||
D、
|
考点:几何概型
专题:应用题,概率与统计
分析:由题意可得,硬币要落在纸板内,硬币圆心距离纸板圆心的距离应该小于7.硬币与小圆无公共点,硬币圆心距离小圆圆心要大于2,先求出硬币落在纸板上的面积,然后再求解硬币落下后与小圆没交点的区域的面积,代入古典概率的计算公式可求.
解答:
解:记“硬币落下后与小圆无公共点”为事件A
硬币要落在纸板内,硬币圆心距离纸板圆心的距离应该小于4,其面积为16π
无公共点也就意味着,硬币的圆心与纸板的圆心相距超过2cm
以纸板的圆心为圆心,作一个半径2cm的圆,硬币的圆心在此圆外面,则硬币与半径为1cm的小圆无公共点,此半径为2的圆面积是4π
所以有公共点的概率为
=
无公共点的概率为P(A)=1-
=
故选:D.
硬币要落在纸板内,硬币圆心距离纸板圆心的距离应该小于4,其面积为16π
无公共点也就意味着,硬币的圆心与纸板的圆心相距超过2cm
以纸板的圆心为圆心,作一个半径2cm的圆,硬币的圆心在此圆外面,则硬币与半径为1cm的小圆无公共点,此半径为2的圆面积是4π
所以有公共点的概率为
| 4 |
| 16 |
| 1 |
| 4 |
无公共点的概率为P(A)=1-
| 1 |
| 4 |
| 3 |
| 4 |
故选:D.
点评:本题主要考查了几何概率的计算公式,用到的知识点为:概率=相应的面积与总面积之比.

练习册系列答案
相关题目
将正整数排列如下:则在表中数字2013出现在( )
1
2 3 4
5 6 7 8 9
10 11 12 13 14 15 16
…
1
2 3 4
5 6 7 8 9
10 11 12 13 14 15 16
…
| A、第44行第78列 |
| B、第45行第78列 |
| C、第44行第77列 |
| D、第45行第77列 |
由若干个相同的正方体叠成的一个物体,它的主视图、左视图、俯视图从左到右分别如图所示,则这个物体共有( )个小正方体.


| A、7 | B、11 | C、12 | D、14 |
已知在△ABC中,
=2
,
=2
,若
=m
+n
,则m+n=( )
| AR |
| RB |
| CP |
| PR |
| AP |
| AB |
| AC |
| A、1 | ||
B、
| ||
C、
| ||
D、
|
将函数f(x)=sin(2x+
)的图象向右平移
个单位后得到函y=g(x)的图象,则g(x)的单调递增区间为( )
| π |
| 3 |
| π |
| 4 |
A、[2kπ-
| ||||
B、[2kπ+
| ||||
C、[kπ-
| ||||
D、[kπ+
|
若m∈R,方程x3-3x+m=0在区间[0,1]上不等的实根( )
| A、有3个 | B、有2个 |
| C、没有 | D、至多有一个 |
一正四棱锥的高为2
,侧棱与底面所成的角为45°,则这一正四棱锥的斜高等于( )
| 2 |
A、2
| ||
B、
| ||
C、2
| ||
D、2
|