��Ŀ����
ij�������ȡ������ij�ֲ�Ʒ200�������������飬����һ��Ʒ126��������Ʒ50��������Ʒ20������Ʒ4������֪����1��һ����������Ʒ��õ�����ֱ�Ϊ6��Ԫ��2��Ԫ��1��Ԫ��������1����Ʒ����2��Ԫ����1����Ʒ������Ϊ�Σ���λ����Ԫ����
������εķֲ��У�
������1����Ʒ��ƽ�����ε���ѧ������
������߲�Ʒ��������Ʒ�ʽ�Ϊ1%��һ��Ʒ����ߵ�70%�������ĸ��ȼ��IJ�Ʒ���������ʱҪ��1����Ʒ��ƽ��������4.74��Ԫ��������Ʒ������Ƕ��٣�
������εķֲ��У�
������1����Ʒ��ƽ�����ε���ѧ������
������߲�Ʒ��������Ʒ�ʽ�Ϊ1%��һ��Ʒ����ߵ�70%�������ĸ��ȼ��IJ�Ʒ���������ʱҪ��1����Ʒ��ƽ��������4.74��Ԫ��������Ʒ������Ƕ��٣�
���㣺��ɢ�������������ֲ���,��ɢ����������������뷽��
ר�⣺������ͳ��
���������ε����п���ȡֵΪ6��2��1��-2���ֱ������Ӧ�ĸ��ʣ��ɴ�������εķֲ��У�
�����ɦεķֲ��������E�Σ�
��������������Ʒ��Ϊx�����ʱ1����Ʒ��ƽ��������Ϊ��E��x��=6��0.7+2����1-0.7-0.01-x��+��-2����0.01+x=4.76-x���ɴ����������Ʒ�������2%��
�����ɦεķֲ��������E�Σ�
��������������Ʒ��Ϊx�����ʱ1����Ʒ��ƽ��������Ϊ��E��x��=6��0.7+2����1-0.7-0.01-x��+��-2����0.01+x=4.76-x���ɴ����������Ʒ�������2%��
���
�⣺���ε����п���ȡֵΪ6��2��1��-2��
P����=6��=
=0.63��
P����=2��=
=0.25��
P����=1��=
=0.1��
P����=-2��=
=0.02��
��εķֲ���Ϊ��
����E��=6��0.63+2��0.25+1��0.1-2��0.02=4.34��
��������������Ʒ��Ϊx�����ʱ1����Ʒ��ƽ��������Ϊ��
E��x��=6��0.7+2����1-0.7-0.01-x��+��-2����0.01+x=4.76-x��
����x��[0��0.29����������֪E��x����4.74��
��4.76-x��4.74��
���x��0.02��
������Ʒ�������2%��
P����=6��=
| 126 |
| 200 |
P����=2��=
| 50 |
| 200 |
P����=1��=
| 20 |
| 200 |
P����=-2��=
| 4 |
| 200 |
��εķֲ���Ϊ��
| �� | 6 | 2 | 1 | -2 |
| P | 0.63 | 0.25 | 0.1 | 0.02 |
��������������Ʒ��Ϊx�����ʱ1����Ʒ��ƽ��������Ϊ��
E��x��=6��0.7+2����1-0.7-0.01-x��+��-2����0.01+x=4.76-x��
����x��[0��0.29����������֪E��x����4.74��
��4.76-x��4.74��
���x��0.02��
������Ʒ�������2%��
���������⿼����ɢ����������ķֲ��к���ѧ�����������е��⣬������߿��ж��DZؿ����ͣ�

��ϰ��ϵ�д�
�����Ŀ
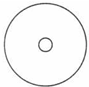 ��ͼ���뾶Ϊ5cm��Բ��ֽ������һ����ͬԲ�ĵİ뾶Ϊ1cm��СԲ���ֽ��뾶Ϊ1cm��һöӲ�Ғ�����ֽ���ϣ�ʹ����Ӳ�������ȫ����ֽ���ڣ���Ӳ����СԲ������ĸ���Ϊ��������
��ͼ���뾶Ϊ5cm��Բ��ֽ������һ����ͬԲ�ĵİ뾶Ϊ1cm��СԲ���ֽ��뾶Ϊ1cm��һöӲ�Ғ�����ֽ���ϣ�ʹ����Ӳ�������ȫ����ֽ���ڣ���Ӳ����СԲ������ĸ���Ϊ��������