题目内容
将函数f（x）=sin（2x+
）的图象向右平移
个单位后得到函y=g（x）的图象，则g（x）的单调递增区间为（ ）
| π |
| 3 |
| π |
| 4 |
A、[2kπ-
| ||||
B、[2kπ+
| ||||
C、[kπ-
| ||||
D、[kπ+
|
考点：函数y=Asin（ωx+φ）的图象变换
专题：三角函数的图像与性质
分析：由函数图象的平移变换得到y=g（x）的图象的解析式，然后由复合函数单调性的求法求解g（x）的单调递增区间．
解答：
解：将函数f（x）=sin（2x+
）的图象向右平移
个单位后得到函y=g（x）的图象的解析式为，
g（x）=sin[2（x-
）+
]=sin（2x-
），
由-
+2kπ≤2x-
≤
+2kπ，得-
+kπ≤x≤
+kπ，k∈Z．
∴g（x）的单调递增区间为[kπ-
，kπ+
]（k∈Z）．
故选：C．
| π |
| 3 |
| π |
| 4 |
g（x）=sin[2（x-
| π |
| 4 |
| π |
| 3 |
| π |
| 6 |
由-
| π |
| 2 |
| π |
| 6 |
| π |
| 2 |
| π |
| 6 |
| π |
| 3 |
∴g（x）的单调递增区间为[kπ-
| π |
| 6 |
| π |
| 3 |
故选：C．
点评：本题考查了y=Asin（ωx+φ）的图象变换，考查了简单的复合函数的单调性的求法，简单的复合函数的单调性满足同增异减的原则，是基础题．
练习册系列答案
相关题目
已知点A、B、C三点不共线，且有
=
=
，则有（ ）
| ||||
| 1 |
| ||||
|
| ||||
|
A、|
| ||||||
B、|
| ||||||
C、|
| ||||||
D、|
|
如果lgx=lga+3lgb-5lgc，那么（ ）
A、x=
| ||
B、x=
| ||
| C、x=a+3b-5c | ||
| D、x=a+b3-c3 |
下列判断错误的是（ ）
A、在△ABC中，“
| ||||||||||||
| B、命题“?x∈R，x2-x-1≤0”的否定是“?x0∈R，x02-x0-1＞0” | ||||||||||||
| C、若p，q均为假命题，则p∧q为假命题 | ||||||||||||
D、若向量
|
设函数f（x）=
，其中[x]表示不超过x的最大整数，如[-1.6]=-2，[1]=1，[1.2]=1，若直线y=kx+1（k＜0）与函数y=f（x）的图象恰有2个不同的交点，则k的取值范围是（ ）
|
A、[-
| ||||
B、[-1，-
| ||||
C、（-1，-
| ||||
D、（-
|
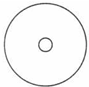如图，半径为5cm的圆形纸板内有一个相同圆心的半径为1cm的小圆，现将半径为1cm的一枚硬币拋到此纸板上，使整块硬币随机完全落在纸板内，则硬币与小圆无公共点的概率为（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
函数y=
的定义域为（ ）
| 2x+6 |
| A、（-∞，-3） |
| B、（-3，+∞） |
| C、（-∞，-3] |
| D、[-3，+∞） |