题目内容
14.在1,1,3,4,5的排列a1,a2,a3,a4,a5中,满足a1<a2,a2>a3,a3<a4,a4>a5的排列个数是8.分析 根据题意,分2种情况,分别求出每种情况下的个数,由分类计数原理计算可得答案.
解答 解:根据题意a2>a1且a2>a3,a4>a3且a4>a5,则a2,a4只能为4,5或3,5.
当a2,a4为4,5时,${A}_{2}^{2}$×3=6种;
当a2,a4为3,5时,只能有45131和13154两种排列方式.
所以总排列个数是8种.
故答案为:8.
点评 本题考查排列组合及简单计数问题,解题的关键是理解含义,进而转化为排列、组合问题.

练习册系列答案
相关题目
5.15名选举人对5名侯选人进行无记名投票选举,若选举人可以投一个至五个候选人的票,也可以弃权,则不同的选举方法共有( )
| A. | 215种 | B. | 275种 | C. | 25种 | D. | 225种 |
19.下列函数中在$(\frac{π}{4},\frac{3}{4}π)$上为减函数的是( )
| A. | y=2cos2x-1 | B. | y=-tanx | C. | $y=cos(2x-\frac{π}{2})$ | D. | y=sin2x+cos2x |
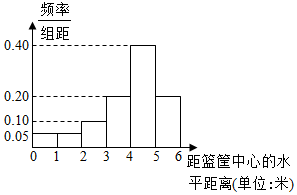 某篮球队对篮球运动员的篮球技能进行统计研究,针对篮球运动员在投篮命中时,运动员在篮筐中心的水平距离这项指标,对某运动员进行了若干场次的统计,依据统计结果绘制如下频率分布直方图:
某篮球队对篮球运动员的篮球技能进行统计研究,针对篮球运动员在投篮命中时,运动员在篮筐中心的水平距离这项指标,对某运动员进行了若干场次的统计,依据统计结果绘制如下频率分布直方图: