Question

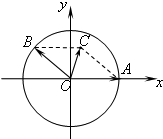如图所示，在xOy平面上，点A（1，0），点B在单位圆上．∠AOB=θ（0＜θ＜π）
（1）若点B（-

3

5

，

4

5

），求tan（2θ+

π

4

）的值；
（2）若

OA

+

OB

=

OC

，四边形OACB的面积用S_四表示，求S_四+

OA

•

OC

的取值范围．

Answer 1

考点：平面向量数量积的运算,单位圆与周期性

专题：计算题,三角函数的求值,平面向量及应用

分析：（1）利用任意角的三角函数定义可得sinθ，cosθ，再利用二倍角的正切公式和两角和的正切公式，计算即可得出；
（2）利用向量的数量积运算法则、平行四边形的面积计算公式可得S_四+

OA

•

OC

的=sinθ+cosθ+1，再利用两角和的正弦公式和正弦函数的性质即可得出．

解答： 解：（1）∵B（-

3

5

，

4

5

），∠AOB=θ，
∴tanθ=

4 5

- 3 5

=-

4

3

∴tan2θ=

2tanθ

1-tan2θ

=

2×(- 4 3 )

1- 16 9

=

24

7

，
则tan（2θ+

π

4

）=

tan2θ+1

1-tan2θ

=

1+ 24 7

1- 24 7

=-

31

17

；
（2）S_四=|OA||OB|sin（π-θ）=sinθ，
∵

OA

=（1，0），

OB

=（cosθ，sinθ），
∴

OC

=

OA

+

OB

=（1+cosθ，sinθ），
∴

OA

•

OC

=1+cosθ，
∴S_四+

OA

•

OC

=sinθ+cosθ+1=

2

sin（θ+

π

4

）+1（0＜θ＜π），
∵

π

4

＜θ+

π

4

＜

5π

4

，
∴-

2

2

＜sin（θ+

π

4

）≤1，
∴0＜S_四+

OA

•

OC

的≤

2

+1．

点评：本题综合考查了任意角的三角函数定义、二倍角公式、两角和差的正切公式、向量的数量积运算法则、平行四边形的面积计算公式、两角和的正弦公式等基础知识与基本技能方法，属于中档题．