题目内容
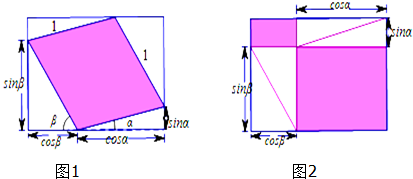
“无字证明”,就是将数学命题用简单、有创意而且易于理解的几何图形来呈现,请利用图1、图2中阴影部分的面积关系,写出该图所验证的一个三角恒等变换公式: .

考点:进行简单的合情推理
专题:推理和证明
分析:左右图中大矩形的面积相等,左边的图中阴影部分的面积为 S1=sin(α+β),在右边的图中,阴影部分的面积 S2 等于2个阴影小矩形的面积之和,等于sinαcosβ+cosαsinβ.而面积 S2 还等于大矩形得面积S 减去2个小空白矩形的面积,再由2个图中空白部分的面积相等,可得S1 =S2 ,从而得出结论.
解答:
解:在左边的图中大矩形的面积S=(cosβ+cosα)(sinβ+sinα)
=sinβcosβ+cosβsinα+cosαsinα+sinβcosα+sinαcosα=sin(α+β)+sinβcosβ+sinαcosα.
用大矩形的面积S减去4个直角三角形的面积就等于阴影部分的面积 S1 .
空白部分的面积等于4个直角三角形的面积,即2×(
sinβcosβ+
sinαcosα)=sinβcosβ+sinαcosα.
故阴影部分的面积 S1 =S-sinβcosβ+sinαcosα=sin(α+β).
而在右边的图中阴影部分的面积 S2 等于2个阴影小矩形的面积之和,即S2=sinαcosβ+cosαsinβ.
在右边的图中大矩形的面积也等于S,S2等于大矩形得面积S 减去2个小空白矩形的面积,
而2个空白矩形的面积之和,即sinβcosβ+sinαcosα,
故左图中空白部分的面积等于右图中空白部分的面积.
故左右图中阴影部分的面积也相等,即 S1 =S2 ,故有sin(α+β)=sinαcosβ+cosαsinβ,
故答案为:sin(α+β)=sinαcosβ+cosαsinβ.
=sinβcosβ+cosβsinα+cosαsinα+sinβcosα+sinαcosα=sin(α+β)+sinβcosβ+sinαcosα.
用大矩形的面积S减去4个直角三角形的面积就等于阴影部分的面积 S1 .
空白部分的面积等于4个直角三角形的面积,即2×(
| 1 |
| 2 |
| 1 |
| 2 |
故阴影部分的面积 S1 =S-sinβcosβ+sinαcosα=sin(α+β).
而在右边的图中阴影部分的面积 S2 等于2个阴影小矩形的面积之和,即S2=sinαcosβ+cosαsinβ.
在右边的图中大矩形的面积也等于S,S2等于大矩形得面积S 减去2个小空白矩形的面积,
而2个空白矩形的面积之和,即sinβcosβ+sinαcosα,
故左图中空白部分的面积等于右图中空白部分的面积.
故左右图中阴影部分的面积也相等,即 S1 =S2 ,故有sin(α+β)=sinαcosβ+cosαsinβ,
故答案为:sin(α+β)=sinαcosβ+cosαsinβ.
点评:本题主要考查三角函数的恒等式的证明,体现了转化的数学思想,属于中档题.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
已知等比数列{an}的公比q>1,且a1a4=8,a2+a3=6,则数列{an}的前n项和Sn=( )
| A、2n |
| B、2n-1 |
| C、2n-1 |
| D、2n-1-1 |
函数f(x)=
的定义域是( )
| x2-4x+3 |
| A、x∈R |
| B、x∈(0,3) |
| C、x∈(1,3) |
| D、x∈(-∞,1]∪[3,+∞) |
已知函数f(x)=
是偶函数,则f(-
)=( )
|
| 1 |
| 4 |
| A、2 | ||
B、
| ||
| C、-2 | ||
D、-
|