题目内容
已知函数f(x)=3+log2x,x∈[1,16],若函数g(x)=[f(x)]2+2f(x2).
(1)求函数g(x)的定义域;
(2)求函数g(x)的最值.
(1)求函数g(x)的定义域;
(2)求函数g(x)的最值.
考点:对数函数的图像与性质
专题:函数的性质及应用
分析:(1)要使函数g(x)的解析式有意义,则
,解得函数g(x)的定义域;
(2)令t=log2x,x∈[1,4],则t∈[0,2],y=g(x)=(t+5)2-10,结合二次函数的图象和性质可得函数g(x)的最值.
|
(2)令t=log2x,x∈[1,4],则t∈[0,2],y=g(x)=(t+5)2-10,结合二次函数的图象和性质可得函数g(x)的最值.
解答:
解:(1)要使函数g(x)的解析式有意义,
则
,
解得x∈[1,4],
故函数g(x)的定义域为[1,4],
(2)令t=log2x,x∈[1,4],
则t∈[0,2],
y=g(x)=[f(x)]2+2f(x2)=(3+log2x)2+2(3+log2x2)=(log2x+5)2-10=(t+5)2-10,
由函数y=(t+5)2-10的图象是开口朝上且以直线t=-5为对称轴的抛物线,
故函数y=(t+5)2-10在[0,2]上单调递增,
故当t=0时,y=g(x)取最小值15,
当t=2,y=g(x)取最大值39,
则
|
解得x∈[1,4],
故函数g(x)的定义域为[1,4],
(2)令t=log2x,x∈[1,4],
则t∈[0,2],
y=g(x)=[f(x)]2+2f(x2)=(3+log2x)2+2(3+log2x2)=(log2x+5)2-10=(t+5)2-10,
由函数y=(t+5)2-10的图象是开口朝上且以直线t=-5为对称轴的抛物线,
故函数y=(t+5)2-10在[0,2]上单调递增,
故当t=0时,y=g(x)取最小值15,
当t=2,y=g(x)取最大值39,
点评:本题考查的知识点是对数函数的图象和性质,二次函数的图象和性质,函数的最值,难度中档.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知正方体ABCD-A1B1C1D1,过顶点A1作平面α,使得直线AC和BC1平面α所成的角都为30°,这样的平面α可以有( )
| A、1个 | B、2个 | C、3个 | D、4个 |
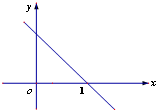 函数f(x)的导数f′(x)的图象是如图所示的一条直线l,l与x轴交点坐标为(1,0),则f(0)与f(2)的大小关系为( )
函数f(x)的导数f′(x)的图象是如图所示的一条直线l,l与x轴交点坐标为(1,0),则f(0)与f(2)的大小关系为( )| A、f(0)<f(2) |
| B、f(0)>f(2) |
| C、f(0)=f(2) |
| D、无法确定 |
设
、
为非零向量,已知命题p:若|
|=2sin
,|
|=4cos
,
•
=1,则
与
的和
;命题q:若函数f(x)=(x
+
)(
-x
)的图象关于y轴对称,则
=
.下列命题正确的是( )
| a |
| b |
| a |
| π |
| 24 |
| b |
| π |
| 24 |
| a |
| b |
| a |
| b |
| π |
| 12 |
| a |
| b |
| a |
| b |
| a |
| b |
| A、p∧q |
| B、p∧(¬q) |
| C、(¬p)∧q |
| D、(¬p)∧(¬q) |