题目内容
8.已知抛物线y2=2px(p>0)上一点M(1,b)到焦点F的距离为2,则b=±2.分析 根据抛物线的定义可知该点到准线的距离为2,进而利用抛物线方程求得其准线方程,利用点到直线的距离求得p,即可得出结论.
解答 解:∵抛物线y2=2px(p>0)上一点M(1,b)到焦点F的距离为2,
∴该点到准线的距离为2,
抛物线的准线方程为x=-$\frac{p}{2}$,
∴1+$\frac{p}{2}$=2,求得p=2,
∴y2=4x,代入点M(1,b),可得b=±2
故答案为:±2.
点评 本题主要考查了抛物线的定义和性质.考查了考生对抛物线定义的掌握和灵活应用,属于基础题.

练习册系列答案
相关题目
18.已知集合 A={-2,-1,0,2,3},B={y|y=|x|,x∈A},则A∩B=( )
| A. | {0,1,2,3} | B. | {2,3} | C. | {0,1,2} | D. | {0,2,3} |
19.已知直线l1:(m-2)x-y+5=0与l2:(m-2)x+(3-m)y+2=0平行,则实数m的值为( )
| A. | 2或4 | B. | 1或4 | C. | 1或2 | D. | 4 |
3.若二次函数f(x)=cx2+4x+a(x∈R)的值域为[0,+∞),则$\frac{1}{a}$+$\frac{9}{c}$的最小值为( )
| A. | 3 | B. | $\frac{9}{2}$ | C. | 5 | D. | 7 |
20.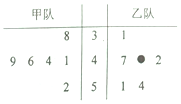 甲乙两个竞赛队都参加了6场比赛,比赛得分情况的经营如图如图(单位:分)),其中乙队的一个得分数字被污损,那么估计乙队的平均得分大于甲队的平均得分的概率为( )
甲乙两个竞赛队都参加了6场比赛,比赛得分情况的经营如图如图(单位:分)),其中乙队的一个得分数字被污损,那么估计乙队的平均得分大于甲队的平均得分的概率为( )
 甲乙两个竞赛队都参加了6场比赛,比赛得分情况的经营如图如图(单位:分)),其中乙队的一个得分数字被污损,那么估计乙队的平均得分大于甲队的平均得分的概率为( )
甲乙两个竞赛队都参加了6场比赛,比赛得分情况的经营如图如图(单位:分)),其中乙队的一个得分数字被污损,那么估计乙队的平均得分大于甲队的平均得分的概率为( )| A. | $\frac{1}{5}$ | B. | $\frac{3}{10}$ | C. | $\frac{2}{5}$ | D. | $\frac{1}{2}$ |
18.已知等差数列{an}前n项和为Sn,若S15=75,a3+a4+a5=12,则S11=( )
| A. | 109 | B. | 99 | C. | $\frac{99}{2}$ | D. | $\frac{109}{2}$ |