题目内容
17.若点A(1,1),B(2,m)都是方程ax2+xy-2=0的曲线上,则m=-1.分析 点A(1,1),B(2,m),代入方程ax2+xy-2=0,解方程组,即可求a、m的值.
解答 解:∵A(1,1),B(2,m)都在方程ax2+xy-2=0的曲线上,
∴$\left\{\begin{array}{l}{a+1-2=0}\\{4a+2m-2=0}\end{array}\right.$,
∴a=1,m=-1,
故答案为:-1
点评 本题考查曲线与方程,考查学生的计算能力,比较基础.

练习册系列答案
相关题目
5.若关于x的方程$\sqrt{-{x}^{2}+4x-3}$=mx+m-1有两个不同的实数根,则实数m的取值范围是( )
| A. | (0,$\frac{3}{4}$) | B. | [$\frac{1}{2}$,$\frac{3}{4}$) | C. | ($\frac{1}{4}$,$\frac{1}{2}$) | D. | [$\frac{1}{4}$,$\frac{3}{4}$) |
9.若集合A={x∈N|5+4x-x2>0},B={x|x<3},则A∩B等于( )
| A. | ∅ | B. | {1,2} | C. | [0,3) | D. | {0,1,2} |
6.斜率为1的直线与抛物线y=ax2(a>0)交于A、B两点,且线段AB的中点C到y轴的距离为1,则该抛物线焦点到准线的距离为( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | 1 | D. | 2 |
7.设m∈R,命题“若m≥0,则方程x2=m有实根”的逆否命题是( )
| A. | 若方程x2=m有实根,则m≥0 | B. | 若方程x2=m有实根,则m<0 | ||
| C. | 若方程x2=m没有实根,则m≥0 | D. | 若方程x2=m没有实根,则m<0 |
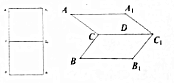 已知:矩形AA1B1B,且AB=2AA1=2,C1,C分别是A1B1、AB的中点,D为C1C中点,将矩形AA1B1B沿着直线C1C折成一个60°的二面角,如图所示.
已知:矩形AA1B1B,且AB=2AA1=2,C1,C分别是A1B1、AB的中点,D为C1C中点,将矩形AA1B1B沿着直线C1C折成一个60°的二面角,如图所示.