题目内容

3．若二次函数f（x）=cx2+4x+a（x∈R）的值域为[0，+∞），则$\frac{1}{a}$+$\frac{9}{c}$的最小值为（　　）
A．3B．$\frac{9}{2}$C．5D．7

分析 先判断a、c是正数，且ac=4，把所求的式子变形使用基本不等式求最小值．

解答 解：若二次函数f（x）=cx2+4x+a（x∈R）的值域为[0，+∞），
则c＞0，△=16-4ac=0，即ac=4，
则 $\frac{1}{a}$+$\frac{9}{c}$≥2×$\sqrt{\frac{9}{ac}}$=3，当且仅当$\frac{1}{a}$=$\frac{9}{c}$时取等号，
则$\frac{1}{a}$+$\frac{9}{c}$的最小值是3，
故选：A．

点评 本题考查函数的值域及基本不等式的应用，求解的关键就是拆项，属于基础题．

练习册系列答案
相关题目
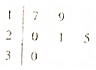13．某车间共有12名工人，随机抽取6名，他们某日加工零件个数的茎叶图如图所示，其中茎为十位数，叶为个位数．
（Ⅰ）根据茎叶图计算样本均值；
（Ⅱ）日加工零件个数大于样本均值的工人为优秀工人，根据茎叶图推断该车间12名工人中有几名优秀工人？
（Ⅲ）在（Ⅱ）的条件下，从该车间12名工人中，任取3人，求恰有1名优秀工人的情况有多少种？
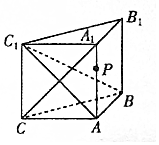14．如图，侧棱垂直于底面的三棱柱ABC-A1B1C1中，AB⊥AC，AA1+AB+AC=3，AB=AC=t（t＞0），P是侧棱AA1上的动点．
（1）当AA1=AB=AC时，求证：A1C⊥BC1；
（2）试求三棱锥P-BCC1的体积V取得最大值时的t值．
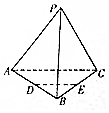11．如图，在正三棱锥P-ABC中，D，E分别是AB，BC的中点．
（1）求证：DE∥平面PAC；
（2）求证：AB⊥PC．
18．抛物线x=2y2的焦点坐标是（　　）
A．（1，0）B．（$\frac{1}{2}$，0）C．（$\frac{1}{8}$，0）D．（0，$\frac{1}{8}$）
8．已知抛物线y2=2px（p＞0）上一点M（1，b）到焦点F的距离为2，则b=±2．
15．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的离心率为$\frac{1}{2}$，椭圆C的四个顶点围成的四边形的面积为4$\sqrt{3}$．
（1）求椭圆C的方程；
（2）直线l与椭圆C交于P（x1，y1），Q（x2，y2）两个不同点，O为坐标原点，若△OPQ的面积为$\sqrt{3}$，证明：y12+y22为定值．
12．已知椭圆中心在原点，焦点在x轴上，离心率e=$\frac{\sqrt{2}}{2}$，顺次连接椭圆四个顶点所得四边形的面积为2$\sqrt{2}$．
（1）求椭圆的标准方程；
（2）已知直线l与椭圆相交于M，N两点，O为原点，若点O在以MN为直径的圆上，试求点O到直线l的距离．
13．命题“?x0∈R，x02+sinx0+e${\;}^{{x}_{0}}$＜1”的否定是（　　）
A．?x0∈R，x02+sinx0+e${\;}^{{x}_{0}}$＞1B．?x0∈R，x02+sinx0+e${\;}^{{x}_{0}}$≥1
C．?x∈R，x2+sinx+ex＞1D．?x∈R，x2+sinx+ex≥1

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网